Parent (previous lemma)
|
Children (=follow up lemmas)
-
is the unknown quantity
 a number, and does the expression in which a number, and does the expression in which  occurs only involve addition, subtraction, multiplication or divisions? ---> Algebraic equation occurs only involve addition, subtraction, multiplication or divisions? ---> Algebraic equation
-
is the unknown quantity
 a number, and does the expression in which a number, and does the expression in which  occurs involve functions that cannot be expressed in finitely many additions, subtractions, multiplications or divisions? In other words, do expressions such as occurs involve functions that cannot be expressed in finitely many additions, subtractions, multiplications or divisions? In other words, do expressions such as 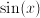 or or 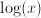 occur in occur in 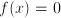 ? ---> Non-algebraic equation ? ---> Non-algebraic equation
-
is the unknown 'quantity' a function and do we know something about its derivative(s)? ---> Differential equation
-
is the unknown 'quantity' a function and do we know something about differences between
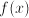 and and 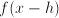 for some for some 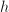 ? ---> Difference equation ? ---> Difference equation
-
is the unknown 'quantity' a function and do we know something about its integral? ---> Integral equation
|
Examples
- Many riddles are equations in disguise: 'when John was five years younger than Suzy, Suzy was twice as old as John' can be expressed as
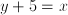 and and 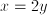 ; it follows that ; it follows that 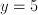 and and 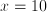 which can be interpreted as the ages of John and Suzy at the time the riddle refers to. Strictly speaking, this is a case of two equations, namely which can be interpreted as the ages of John and Suzy at the time the riddle refers to. Strictly speaking, this is a case of two equations, namely 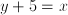 and and 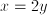 , with two unknowns, namely , with two unknowns, namely  and and 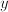 . The unknown, in this case, is therefore a set of two numbers, . The unknown, in this case, is therefore a set of two numbers,  and and 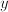 . Both equations have to hold for one pair of values for . Both equations have to hold for one pair of values for  and and 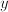 , hence the name 'simultaneous equations'. , hence the name 'simultaneous equations'.
- Most physical and economical laws come in the form of equations. These relate quantities, but they not necessarily express the quantity you are interested in as a function of known quantities. To obtain functional dependencies, equations need to be solved. For instance, Ohms law is usually stated
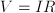 . Suppose that you need to know . Suppose that you need to know 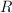 to ensure that, given a voltage to ensure that, given a voltage 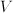 , a current , a current 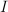 results. Then you need to 'solve' results. Then you need to 'solve' 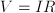 , treating , treating 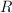 as an unknown. The solution is the function as an unknown. The solution is the function 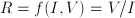 . In this case the solution could be obtained in closed form. That is: there is a function, involving only additions, multiplications, divisions and subtractions, that expresses . In this case the solution could be obtained in closed form. That is: there is a function, involving only additions, multiplications, divisions and subtractions, that expresses 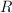 in terms of the known quantities. Most often, equations cannot be solved in closed form: numerical approximtion is needed in stead. in terms of the known quantities. Most often, equations cannot be solved in closed form: numerical approximtion is needed in stead.
|
 between quantities
between quantities  and
and 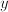 is denoted as
is denoted as 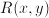 , where
, where  and
and 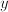 can be arbitrary quantities. Sometimes, a relation is denoted by
can be arbitrary quantities. Sometimes, a relation is denoted by 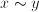 if we consider only one relation, or
if we consider only one relation, or 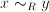 if the relation
if the relation 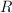 should be distinguished from other relations.
should be distinguished from other relations.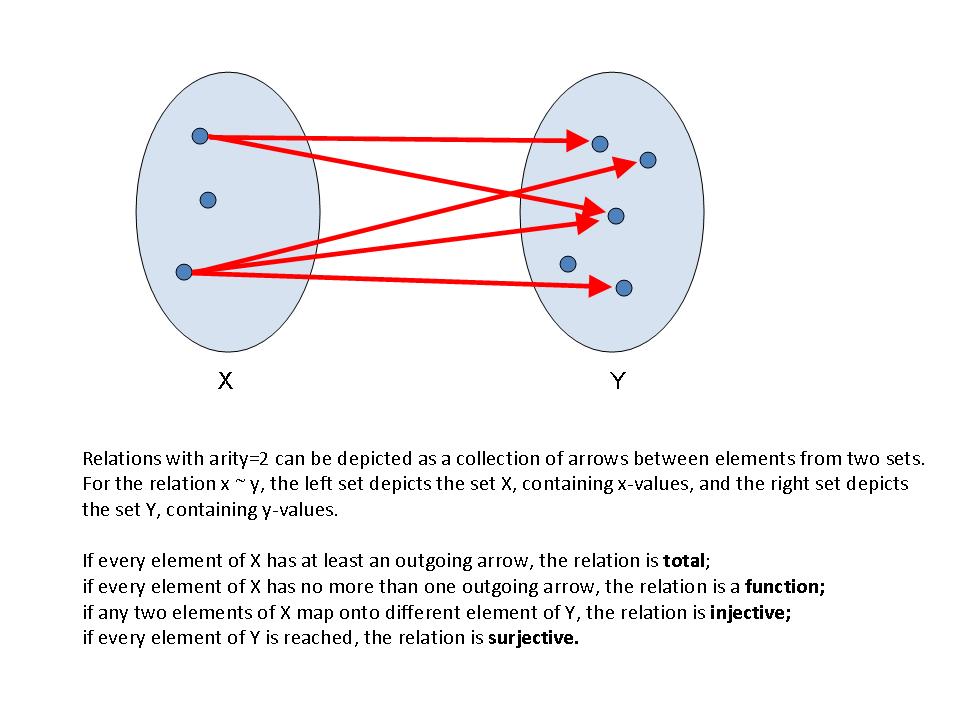
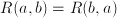 ; a reflecive relation means than
; a reflecive relation means than 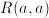 holds for any
holds for any  ; a transitive relation means that
; a transitive relation means that 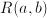 and
and 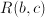 implies that
implies that 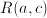 .
.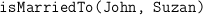 , or
, or 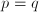 . Both are symmetric. Examples of arity=3 are
. Both are symmetric. Examples of arity=3 are 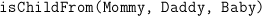 , or
, or 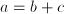 . Definitions of symmetry, reflexiveness and transitivity don't straightforwardly generalize to arities larger than 2.
. Definitions of symmetry, reflexiveness and transitivity don't straightforwardly generalize to arities larger than 2.
 between a lens with focal length
between a lens with focal length  and a screen, what should the distance
and a screen, what should the distance  between the object and the lens be so that the image is sharp? The theoretical relationship between
between the object and the lens be so that the image is sharp? The theoretical relationship between 
 ;
; 
 of a propery
of a propery  for a concept
for a concept 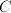 is a function of that concept:
is a function of that concept: 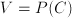 , for instance the population (=a number) of a country is a function of that country: any other country might have another population. Similar, the dominant export product (although not a number) of a country is also a function of that country.
, for instance the population (=a number) of a country is a function of that country: any other country might have another population. Similar, the dominant export product (although not a number) of a country is also a function of that country. is the set of reals, the range is the set of reals between -1 and 1.
is the set of reals, the range is the set of reals between -1 and 1. Monday, Tuesday, ..., Sunday
Monday, Tuesday, ..., Sunday  .
.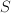 is the number that, multiplied with itself, yields
is the number that, multiplied with itself, yields 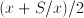 . In this case, the recipe to compute the function value does not terminate, but if we need only the first few decimals of the answer, this is an efficient way to do so.
. In this case, the recipe to compute the function value does not terminate, but if we need only the first few decimals of the answer, this is an efficient way to do so.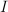 through a resistor
through a resistor 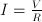 , which is a function of
, which is a function of 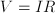 , which is a function of
, which is a function of 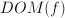 ;
;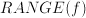 .
.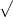 ,
, 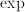 can only be numerically approximated. Still, we commonly work with such functions. First, because analytic results exist that allow to rewrite functions into other expressions, even if we cannot evaluate such functions. For instance,
can only be numerically approximated. Still, we commonly work with such functions. First, because analytic results exist that allow to rewrite functions into other expressions, even if we cannot evaluate such functions. For instance, 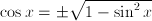 . Further, if the answer to a problem is given in terms of functions of known quantities, where these functions can be numerically approximated to arbitrary precision, we usually say that the problem is solved. In modeling, we assume that the recipe to (approximately) evaluate a function
. Further, if the answer to a problem is given in terms of functions of known quantities, where these functions can be numerically approximated to arbitrary precision, we usually say that the problem is solved. In modeling, we assume that the recipe to (approximately) evaluate a function 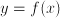 can be implemented on a computer in order to give a numerical approximation to y.
can be implemented on a computer in order to give a numerical approximation to y.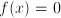 : an equation with unknown quantity
: an equation with unknown quantity 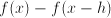 it is called a diffrence equation.
it is called a diffrence equation.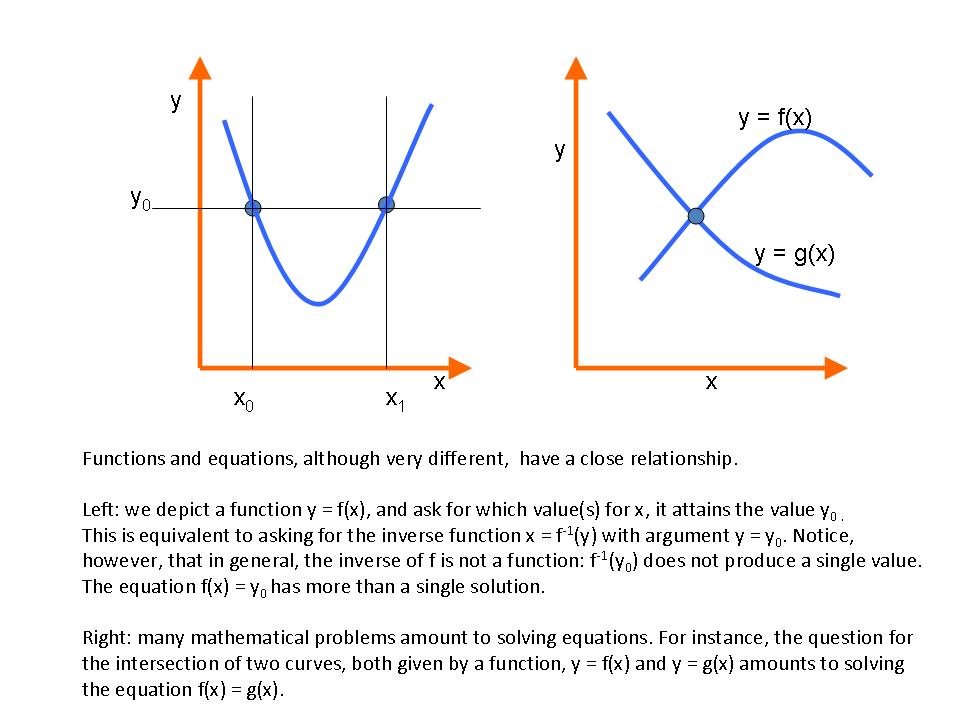
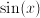 or
or 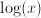 occur in
occur in 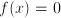 ? --->
? ---> 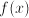 and
and 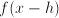 for some
for some 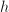 ? --->
? ---> 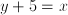 and
and 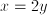 ; it follows that
; it follows that 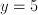 and
and 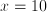 which can be interpreted as the ages of John and Suzy at the time the riddle refers to. Strictly speaking, this is a case of two equations, namely
which can be interpreted as the ages of John and Suzy at the time the riddle refers to. Strictly speaking, this is a case of two equations, namely 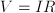 . Suppose that you need to know
. Suppose that you need to know 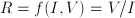 . In this case the solution could be obtained in closed form. That is: there is a function, involving only additions, multiplications, divisions and subtractions, that expresses
. In this case the solution could be obtained in closed form. That is: there is a function, involving only additions, multiplications, divisions and subtractions, that expresses  . Solving the equation is the same as finding an inverse
. Solving the equation is the same as finding an inverse  for the function
for the function 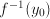 . This inverse, however, not always exists in the form of a single function. The function
. This inverse, however, not always exists in the form of a single function. The function 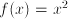 , for instance, occurring in the equation
, for instance, occurring in the equation 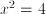 , has two corresponding inverse functions:
, has two corresponding inverse functions: 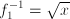 and
and 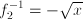 , leading to the two solutions of the equation, 2 and -2.
, leading to the two solutions of the equation, 2 and -2. 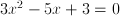 . Also cases where more than one unknown occurs classify as algebraic equations, such as
. Also cases where more than one unknown occurs classify as algebraic equations, such as 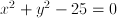 . The equation is solved, in case of one unknown
. The equation is solved, in case of one unknown 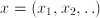 and
and 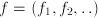 .
If
.
If 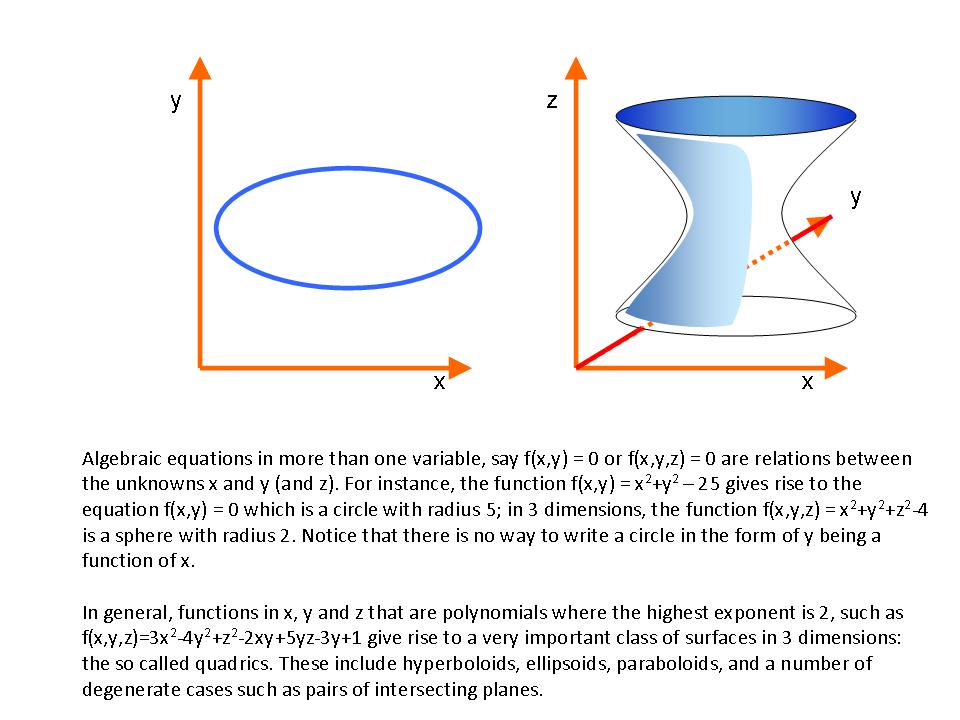
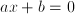 , for
, for 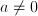 with solution
with solution 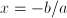 . In case
. In case 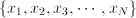 , and
, and 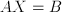 where
where 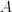 is a
is a 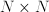 matrix, and
matrix, and 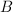 and
and 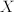 are
are 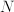 -dimensional vectors. The formal solution is
-dimensional vectors. The formal solution is 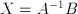 , where
, where 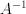 is the inverse matrix of
is the inverse matrix of 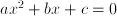 , is solved in closed form by the abc-formula:
, is solved in closed form by the abc-formula: 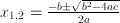 .
.
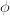 , defined as
, defined as 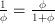 with solution
with solution 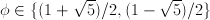 .
.
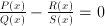 can always be re-written to polynomial equations, as in this case:
can always be re-written to polynomial equations, as in this case: 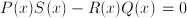 by left and right multiplying with the product of the denominators.
by left and right multiplying with the product of the denominators. 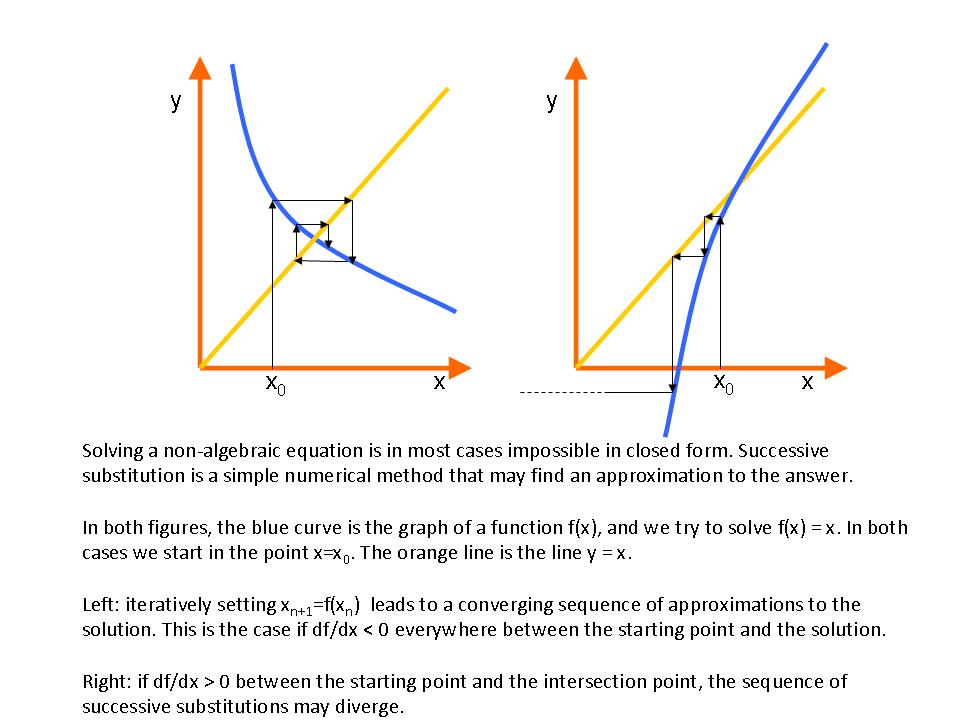
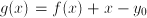 . Then the original equation,
. Then the original equation, 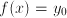 becomes
becomes 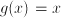 . Start with a guess for
. Start with a guess for 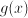 . If the sequence of
. If the sequence of  years, the growth rate is
years, the growth rate is 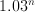 . So
. So 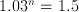 , and therefore
, and therefore 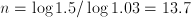 . Conversely, I could ask 'how much interest rate is required if I want this growth to occur in 10 years?'; the answer then is
. Conversely, I could ask 'how much interest rate is required if I want this growth to occur in 10 years?'; the answer then is 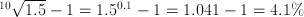 .
. . We need to have
. We need to have  or
or 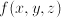 is called a partial differential equation or PDE for short. An ODE or PDE is linear if
is called a partial differential equation or PDE for short. An ODE or PDE is linear if 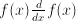 or
or 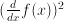 makes the differential equation non-linear. A homogeneous differential equation contains no terms that don't contain
makes the differential equation non-linear. A homogeneous differential equation contains no terms that don't contain 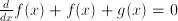 . Coefficients in a differential equation can be constant, as in
. Coefficients in a differential equation can be constant, as in 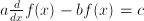 ; a differential equation of the form
; a differential equation of the form 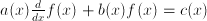 has non-constant coefficients.
has non-constant coefficients.
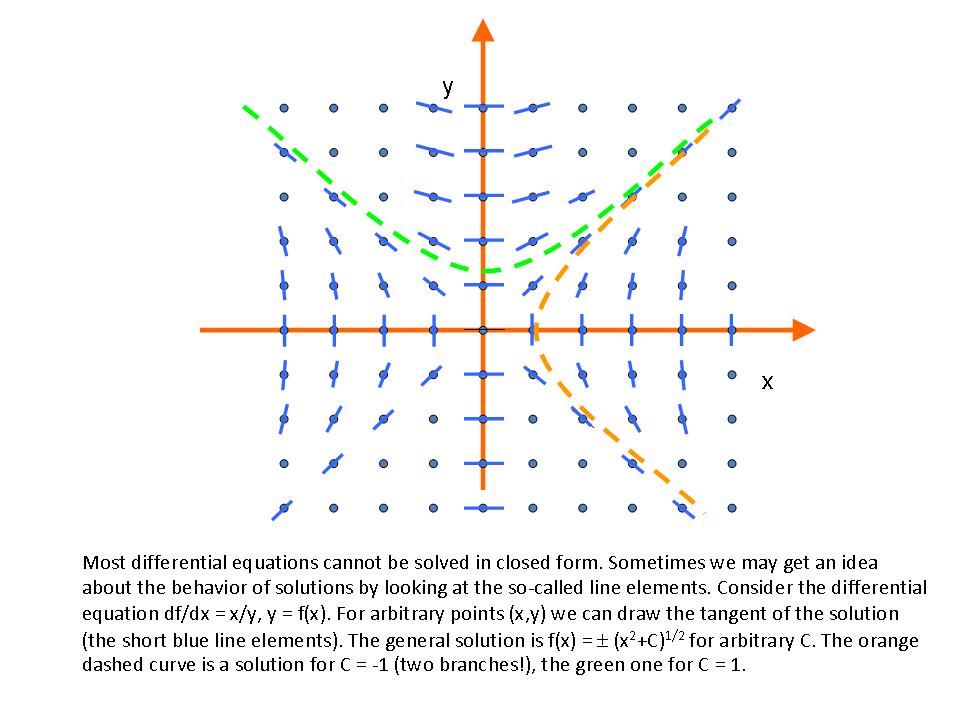
 as a function of time
as a function of time 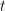 . Often, we don't know
. Often, we don't know 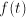 immediately, but we know something about derivatives of
immediately, but we know something about derivatives of 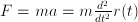 .
. 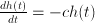 ,
, 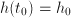 , where
, where 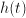 is the water level and
is the water level and  relates to the size of the opening.
relates to the size of the opening.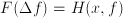 , where
, where 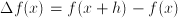 . Just as with differential equations, where second order derivatives,
. Just as with differential equations, where second order derivatives, 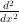 of the unknown function occur, we have second order differences:
of the unknown function occur, we have second order differences: 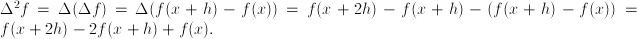 Another name for difference equations is recurrence relations.
Another name for difference equations is recurrence relations.
 (notice the additional term
(notice the additional term 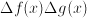 ). The quotient rule reads:
). The quotient rule reads: 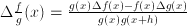 .
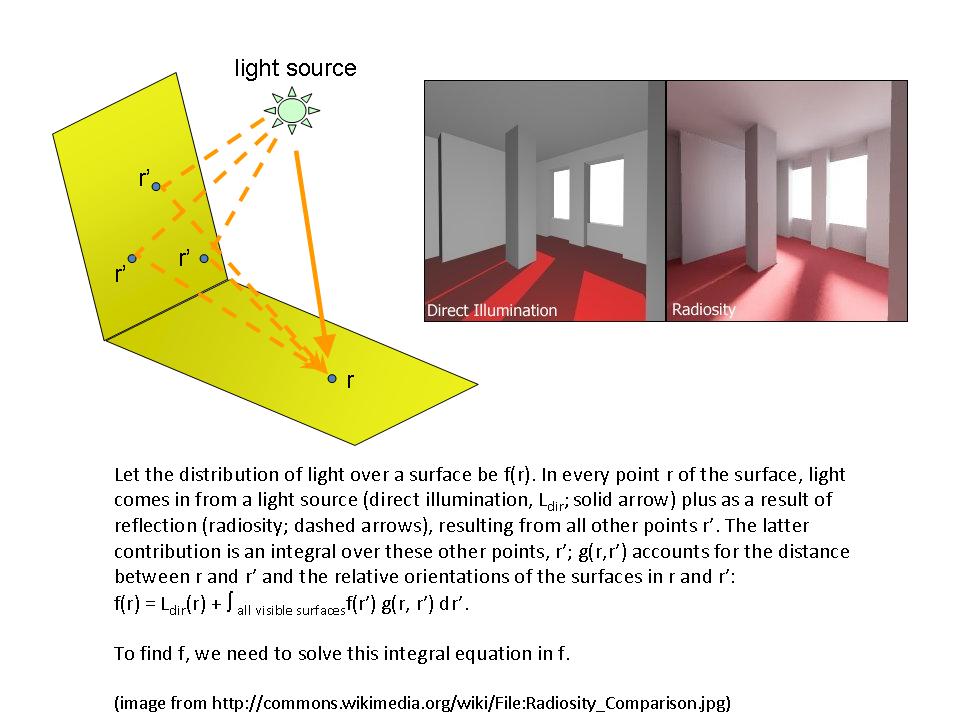
.
 (often, there are multiple
(often, there are multiple 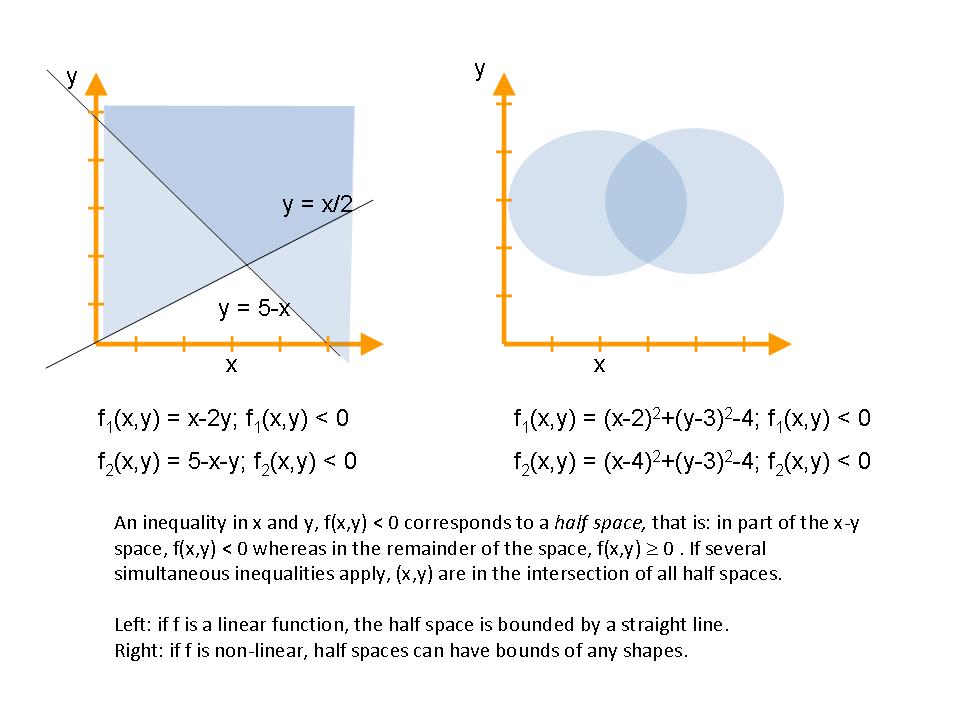
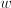 , height
, height 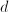 , this problem reads: what is the maximum of
, this problem reads: what is the maximum of 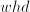 , where the inequality
, where the inequality 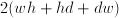 <
< 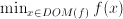 , subject to
, subject to 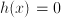 and/or
and/or 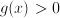 where there can be multiple
where there can be multiple 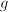 's. There is only one numeric function
's. There is only one numeric function 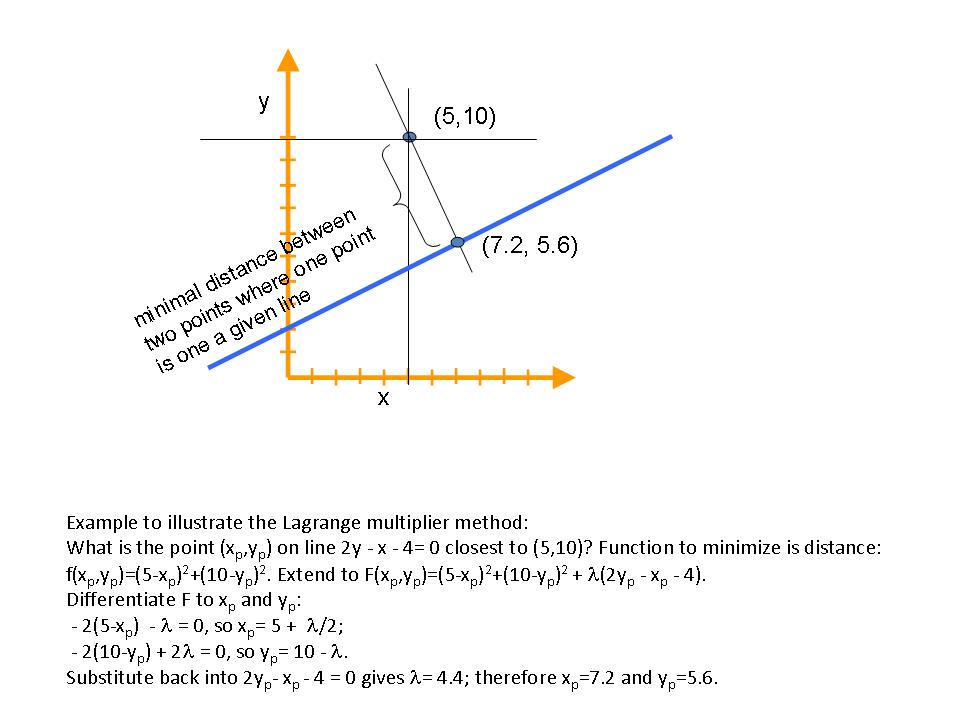
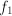 ,
, 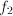 , … to be optimal (e.g. highest efficiency and lowest price), we can form a penalty function,
, … to be optimal (e.g. highest efficiency and lowest price), we can form a penalty function, 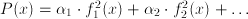 and minimize
and minimize 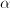 determine relative importances of the various criteria
determine relative importances of the various criteria 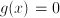 , we can apply the so-called Lagrange multiplier method, see
, we can apply the so-called Lagrange multiplier method, see 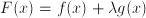 , and find an extreme of
, and find an extreme of 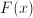 . Call this extreme
. Call this extreme 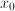 ; in general,
; in general, 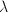 . In order to establish the value of
. In order to establish the value of 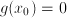 . Solve this equation for
. Solve this equation for 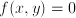 (equation), from
(equation), from 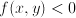 (inequality) or from
(inequality) or from 
 as expensive as the wine; what does the wine cost (equation)?
as expensive as the wine; what does the wine cost (equation)? ) and sets are combined using set theory (
) and sets are combined using set theory (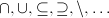 )
)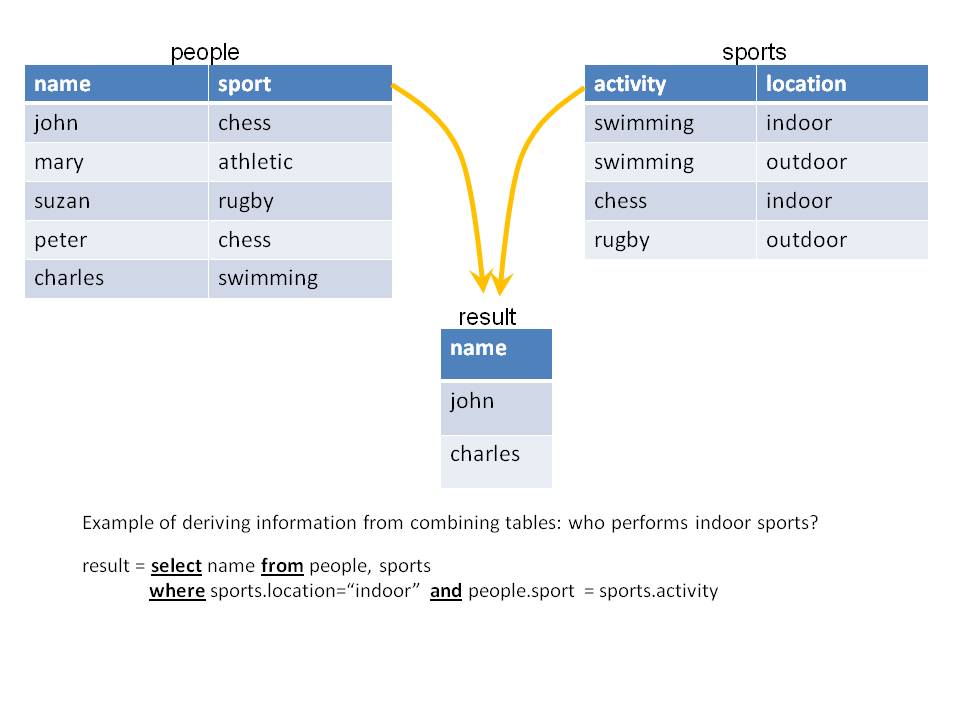
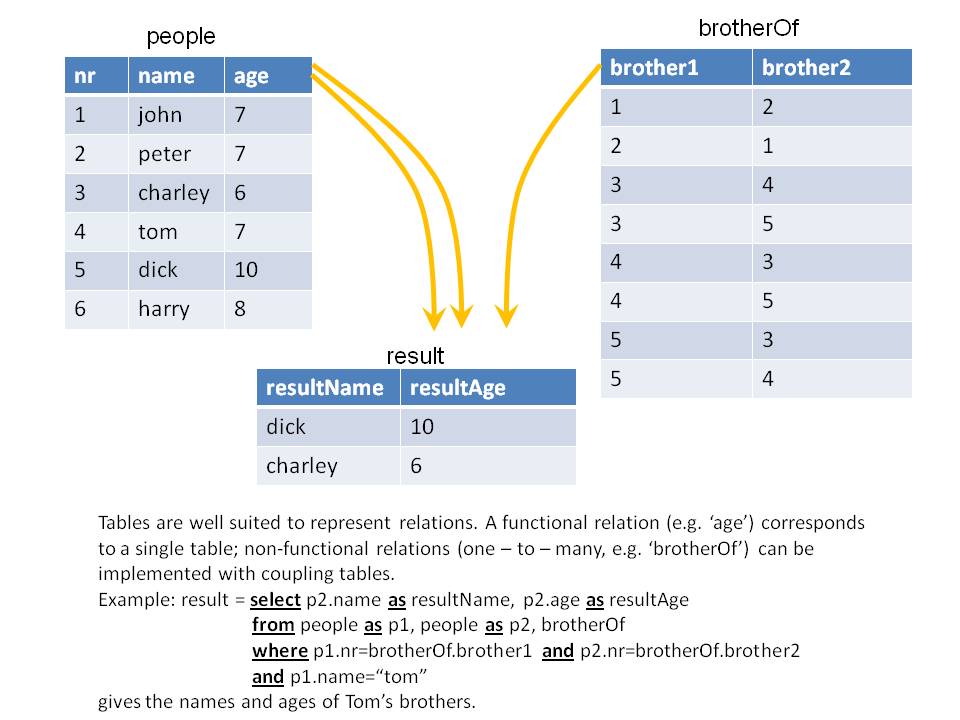
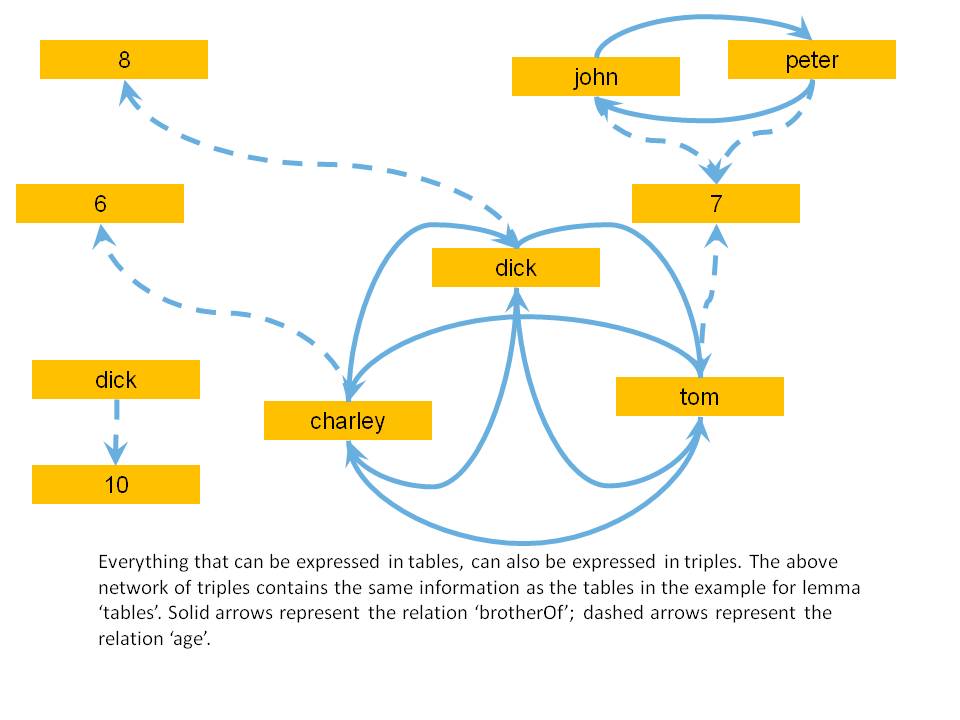
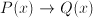 , where
, where 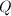 are predicates over dummy quantity
are predicates over dummy quantity 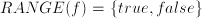 : so called predicates.
: so called predicates.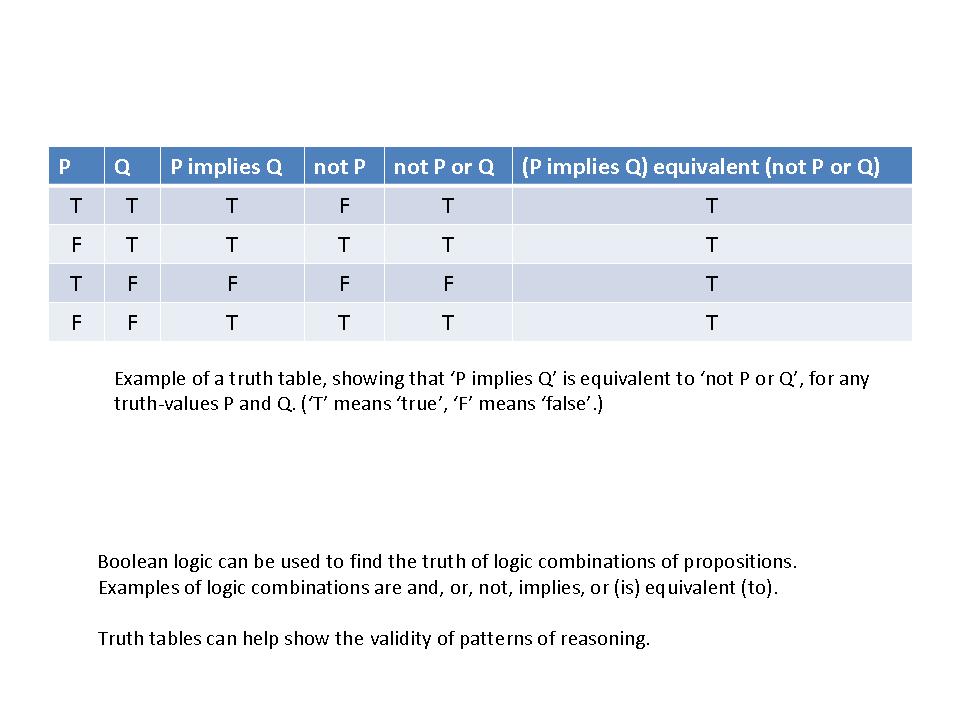
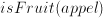 and rule1:
and rule1: 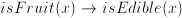 . Then we can deduce (= assess the truth of)
. Then we can deduce (= assess the truth of) 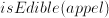 . With more extensive sets of facts and rules, we can have an automated inference system to help us e.g. drawing medical diagnoses or trouble shooting complex apparatus.
. With more extensive sets of facts and rules, we can have an automated inference system to help us e.g. drawing medical diagnoses or trouble shooting complex apparatus.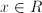 and
and 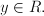 (Functions where
(Functions where 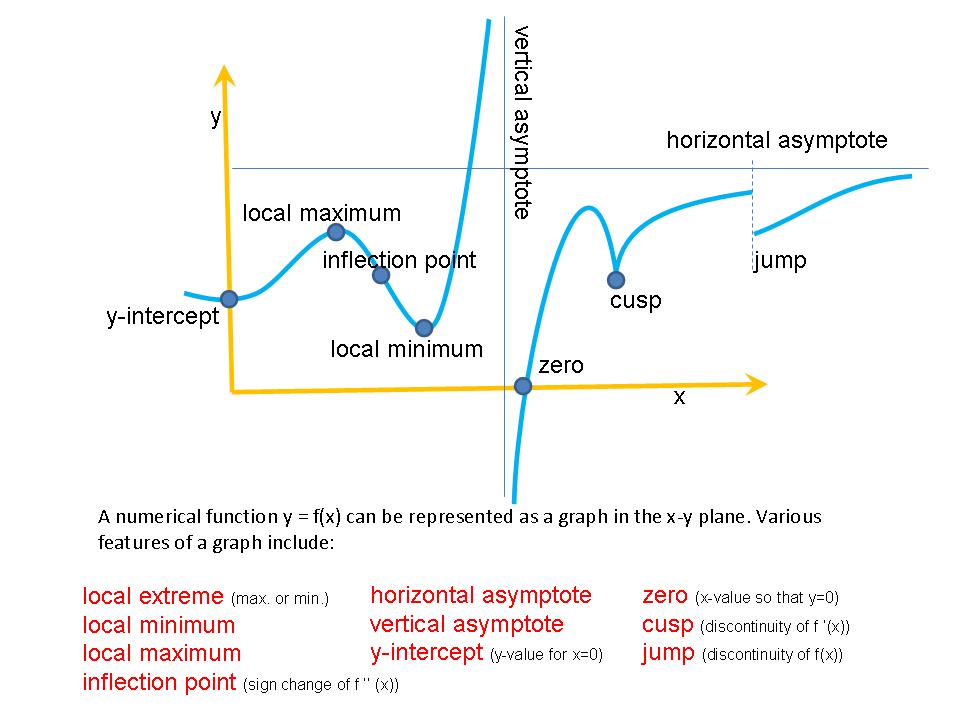
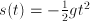 ), the volume of geometric objects are functions of their size, etc.
), the volume of geometric objects are functions of their size, etc.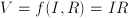 ;
; 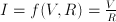 ;
; 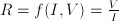 .
.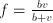 . This could also be
. This could also be 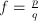 , where
, where 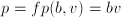 and
and 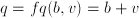 . The latter functions are simpler, but quantities
. The latter functions are simpler, but quantities 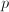 and
and 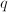 have no immediate meaning. Developing functions is often a trade-off between simplicity and meaning.
have no immediate meaning. Developing functions is often a trade-off between simplicity and meaning.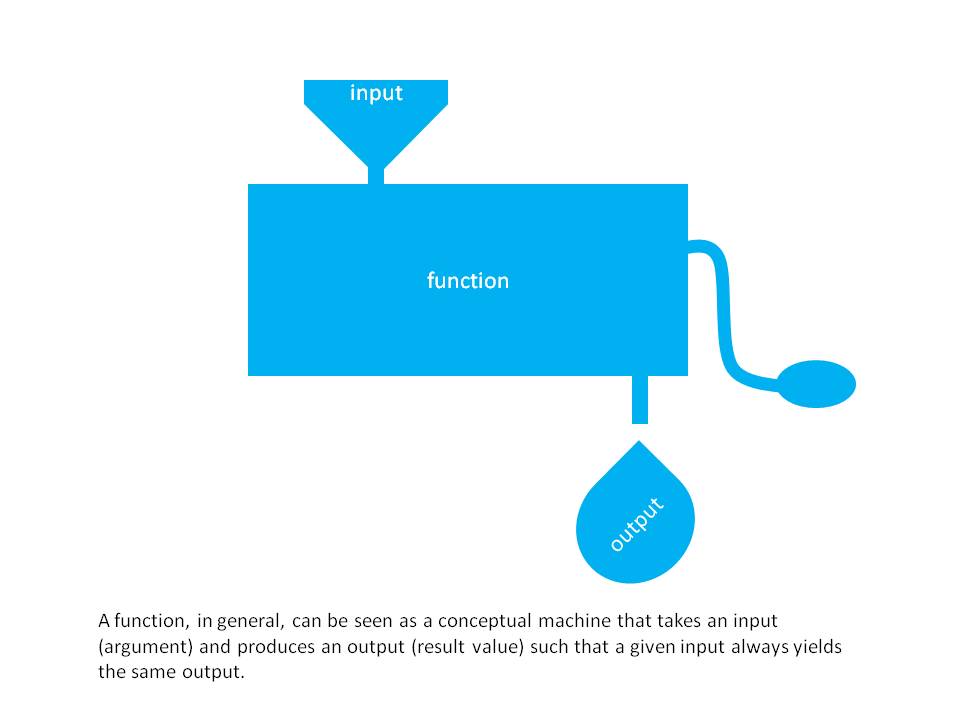
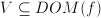
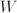 , descend as a function of the year
, descend as a function of the year 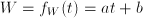 , with
, with  . This only makes sense for
. This only makes sense for  .
.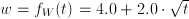 ,
, 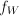 is meaningless (say) for
is meaningless (say) for 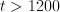 and for
and for  .
.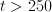 ). The lower bound
). The lower bound 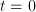 , however, comes from the used mathematical expression (
, however, comes from the used mathematical expression (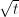 is undefined for
is undefined for 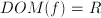 , we can study features such as asymptotes (=the behavior of a function for the argument going to infinity).
, we can study features such as asymptotes (=the behavior of a function for the argument going to infinity).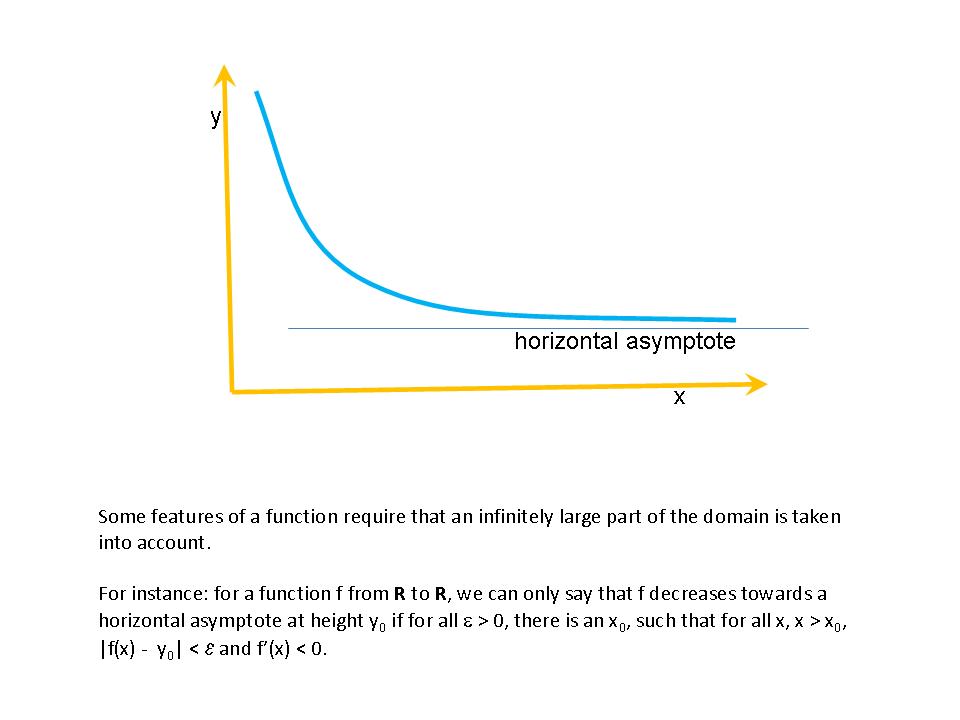
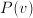 , say, of finding value
, say, of finding value 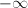 to
to 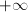 is equal to 1.
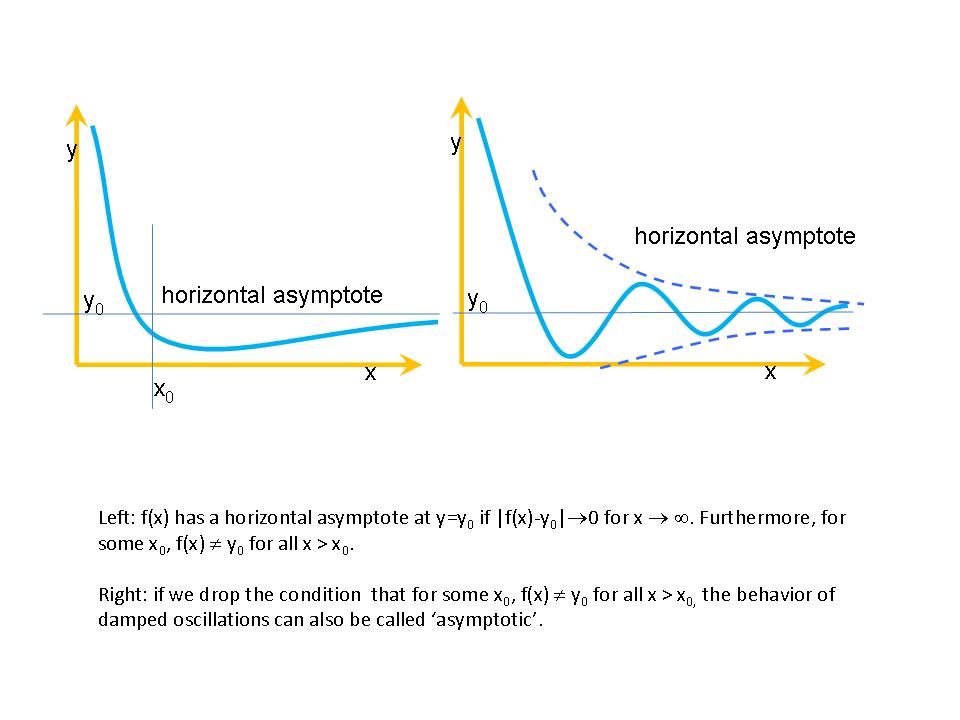
is equal to 1.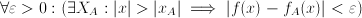
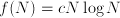 for constant
for constant 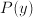 holds.
holds.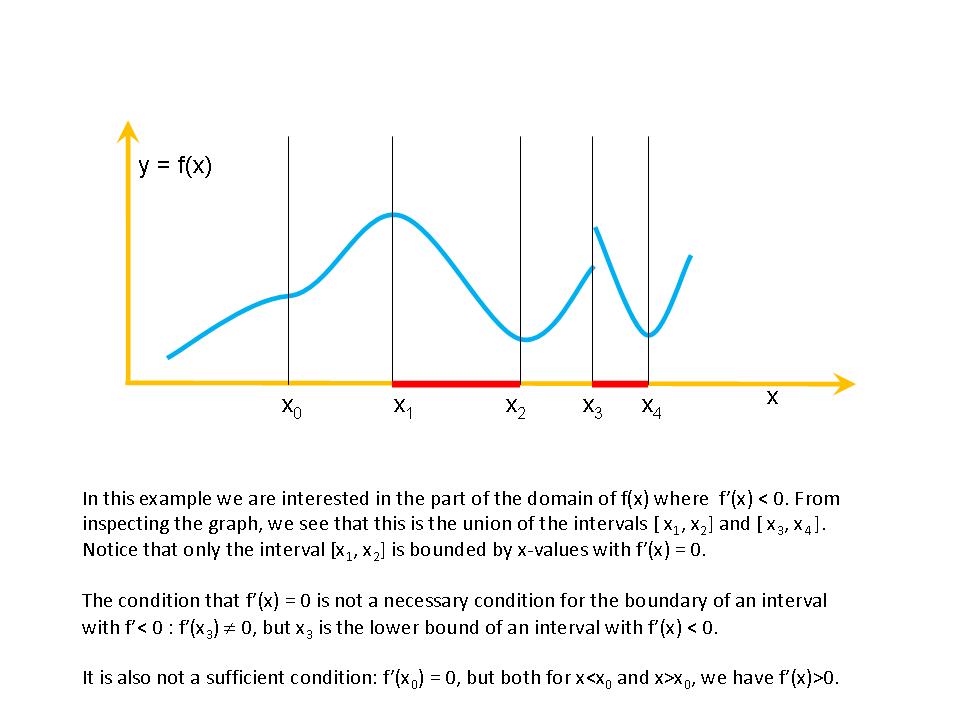
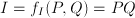 where
where 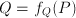 . We may ask the range of prices such that
. We may ask the range of prices such that 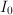 .
.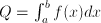
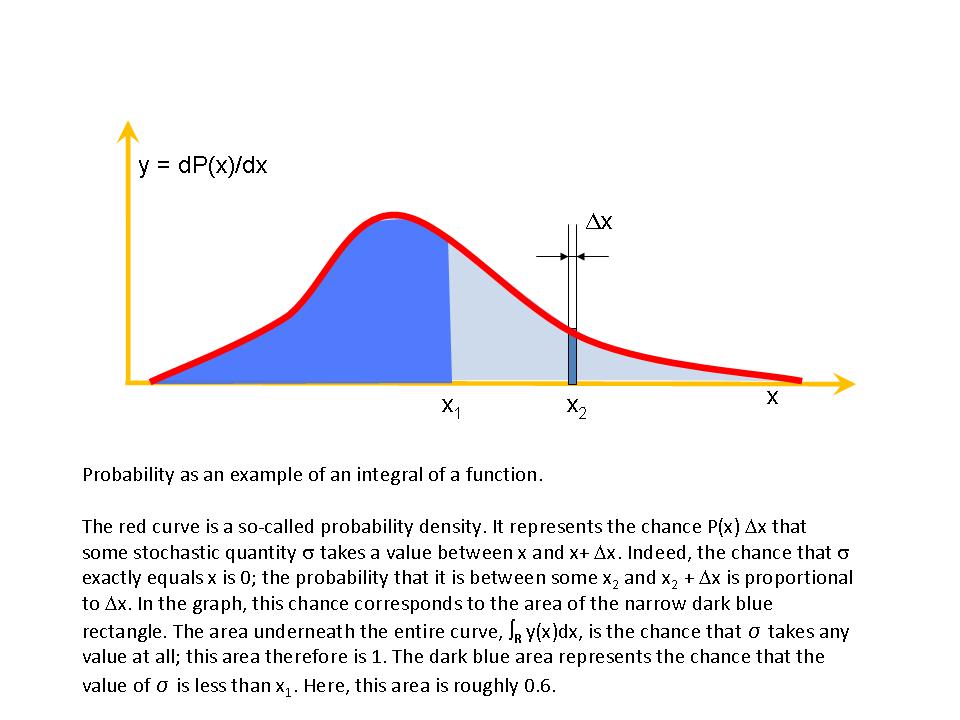
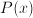 is a function that tells, for some quantity, how large the chance is that its value will be between
is a function that tells, for some quantity, how large the chance is that its value will be between 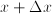 (for
(for 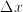 sufficiently small). So, the chance that
sufficiently small). So, the chance that 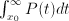 , and the fact that it is certain that
, and the fact that it is certain that 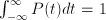 .
. , and
, and 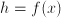 is the height of some interestingly shaped wall (
is the height of some interestingly shaped wall (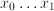 of the wall we can paint, we have that
of the wall we can paint, we have that 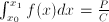 . This can be used, e.g., to find
. This can be used, e.g., to find 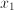 for given
for given 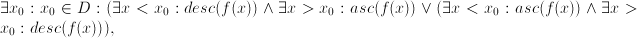 where
where 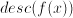 means:
means: 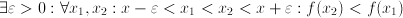 . Similar for
. Similar for 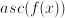 .
.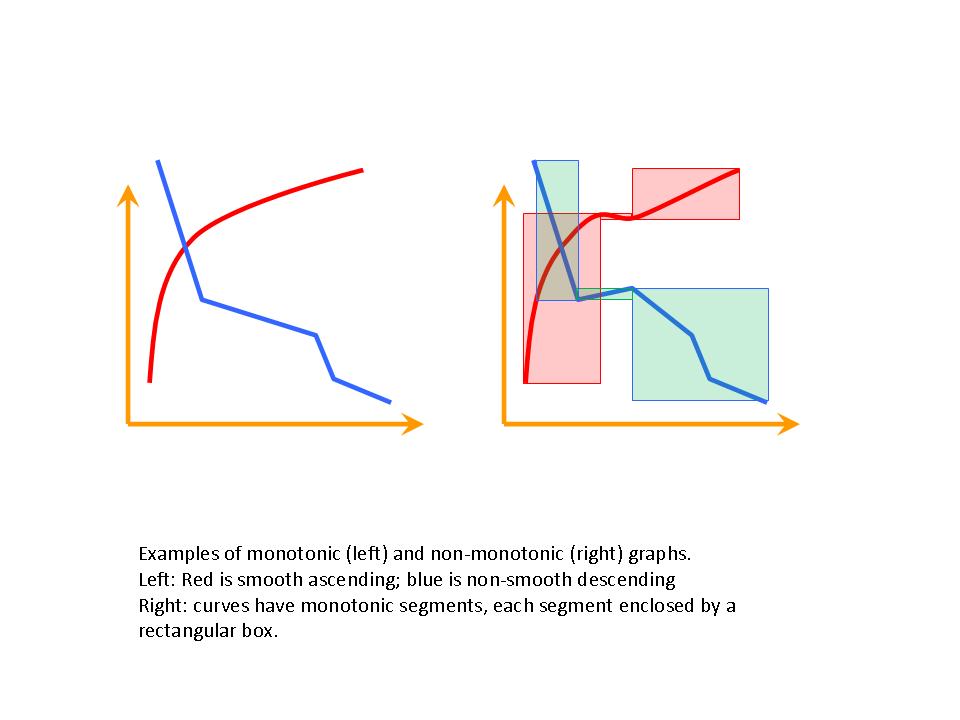
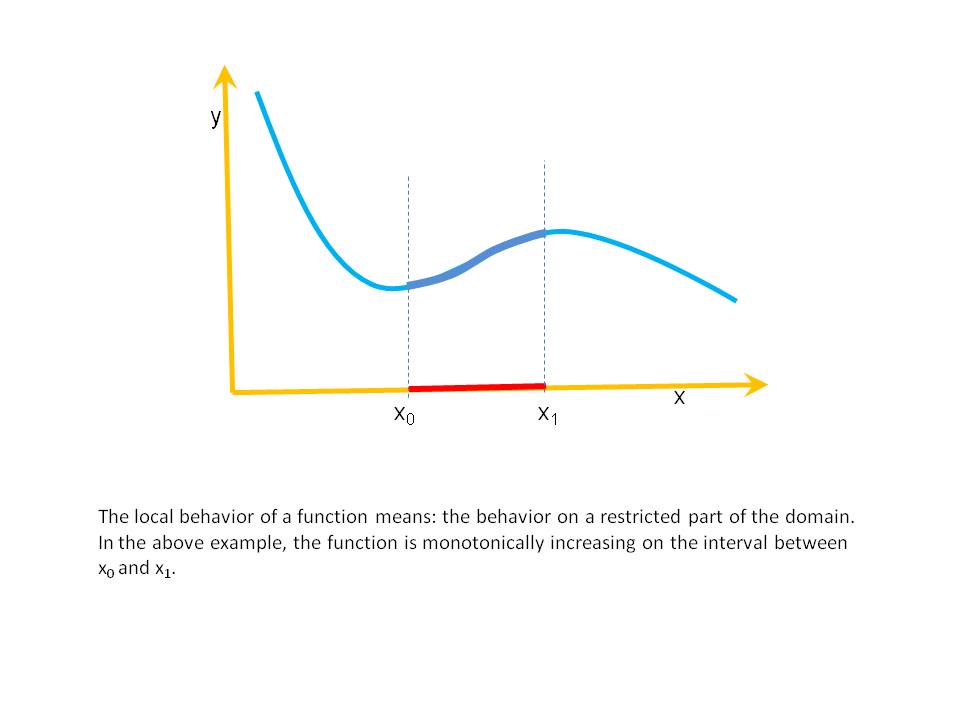
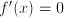 ) which is a local extreme (a local maximum or a local minimum). An example of a non-smooth function that is monotonic (i.e., descends everywhere) is
) which is a local extreme (a local maximum or a local minimum). An example of a non-smooth function that is monotonic (i.e., descends everywhere) is 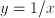 : it is non-smooth in
: it is non-smooth in 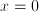 ; notice that
; notice that 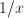 has no local extrema.
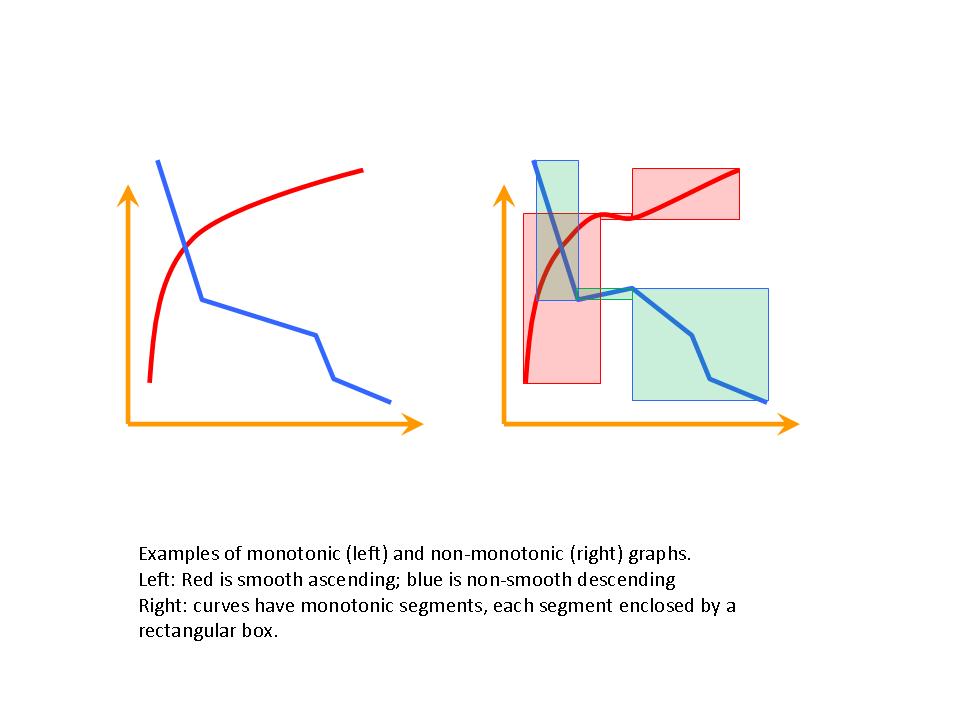
has no local extrema.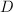 , either ascends (increases) or descends (decreases) for all
, either ascends (increases) or descends (decreases) for all 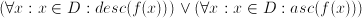
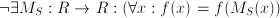 , where
, where 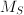 is a symmetry mapping (such as rotation, translation, …) (notice: there is no simple intensional definition of the collection of symmetry mappings).
is a symmetry mapping (such as rotation, translation, …) (notice: there is no simple intensional definition of the collection of symmetry mappings).
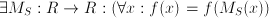 , where
, where 
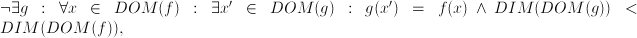 where
where 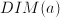 is the dimension of
is the dimension of 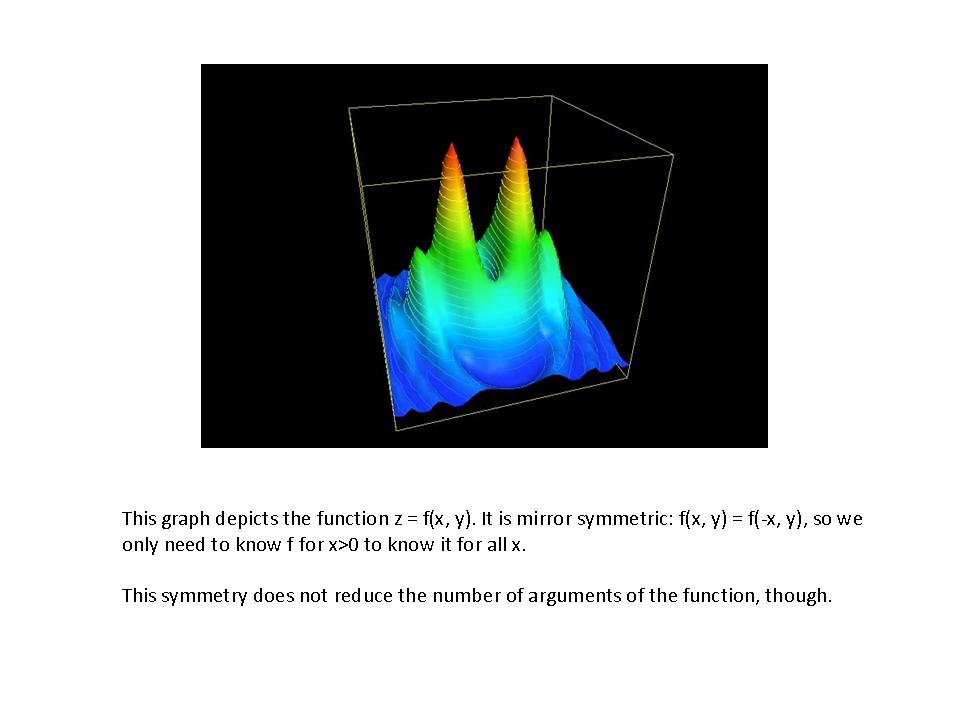
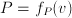 to move a fluid through a pipe with speed
to move a fluid through a pipe with speed 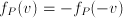 .
. ,
, 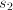 and ages
and ages 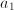 ,
, 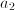 are neighbours is
are neighbours is 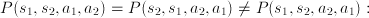 the function
the function 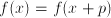 for some
for some 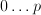 and the entire set of real numbers
and the entire set of real numbers 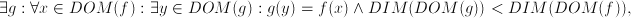 where
where 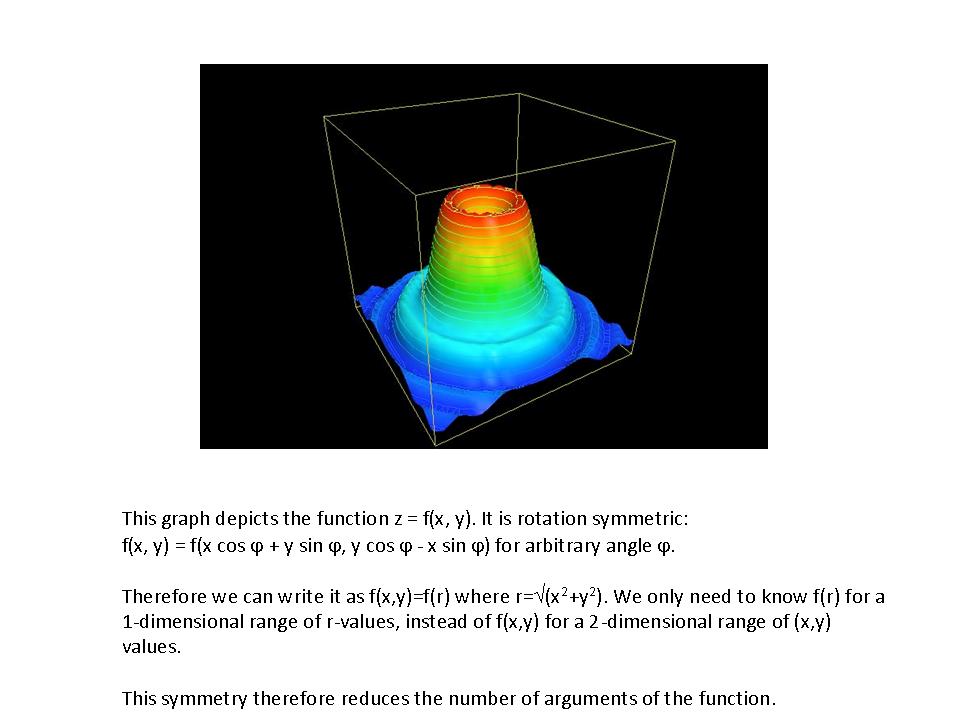
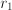 and
and 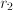 only depends on the difference
only depends on the difference  (3 instead of 6 dimensions); the strength of this interaction only depends on
(3 instead of 6 dimensions); the strength of this interaction only depends on 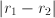 (1 instead of 6 dimensions).
(1 instead of 6 dimensions).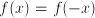 , or, in general:
, or, in general: 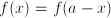 for some
for some 
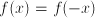 are called even. Examples are
are called even. Examples are  . Functions such as
. Functions such as 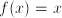 ,
, 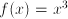 ,
, 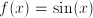 have the property that
have the property that 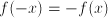 . These are not mirror symmetric (they are called odd), but they could be called symmetric in the sense that knowledge of their behavior on part of the domain informs us about their behavior on the entire domain.
. These are not mirror symmetric (they are called odd), but they could be called symmetric in the sense that knowledge of their behavior on part of the domain informs us about their behavior on the entire domain.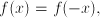 the derivative
the derivative 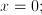 the value
the value 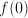 can be arbitrary.
can be arbitrary.
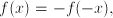 the derivative
the derivative 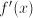 for
for 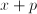 gives the same result. We can repeat this:
gives the same result. We can repeat this: 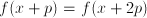 , and so on, so such functions repeat themselves on the entire domain.
, and so on, so such functions repeat themselves on the entire domain.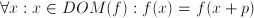 for some constant
for some constant 
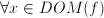 ,
, 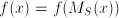 .
..jpg)
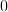 ,
, 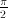 ,
,  , or
, or 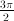 .
.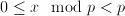 for integer
for integer 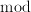 (from ‘modulo’) is the remainder by division.
(from ‘modulo’) is the remainder by division.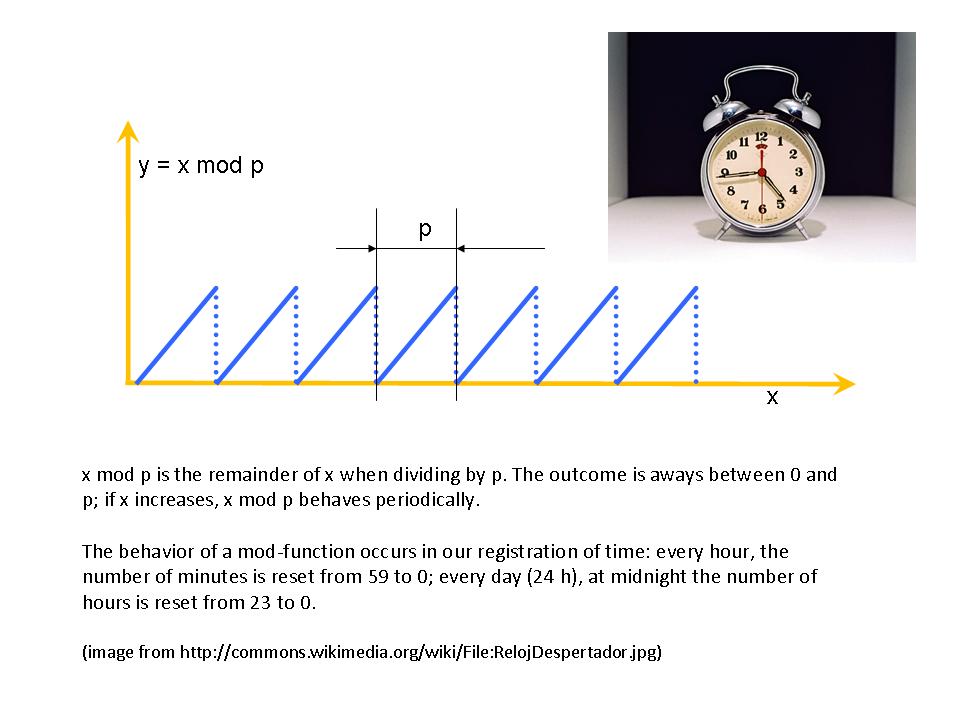
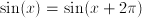 ,
, 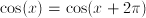 ,
, 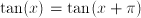
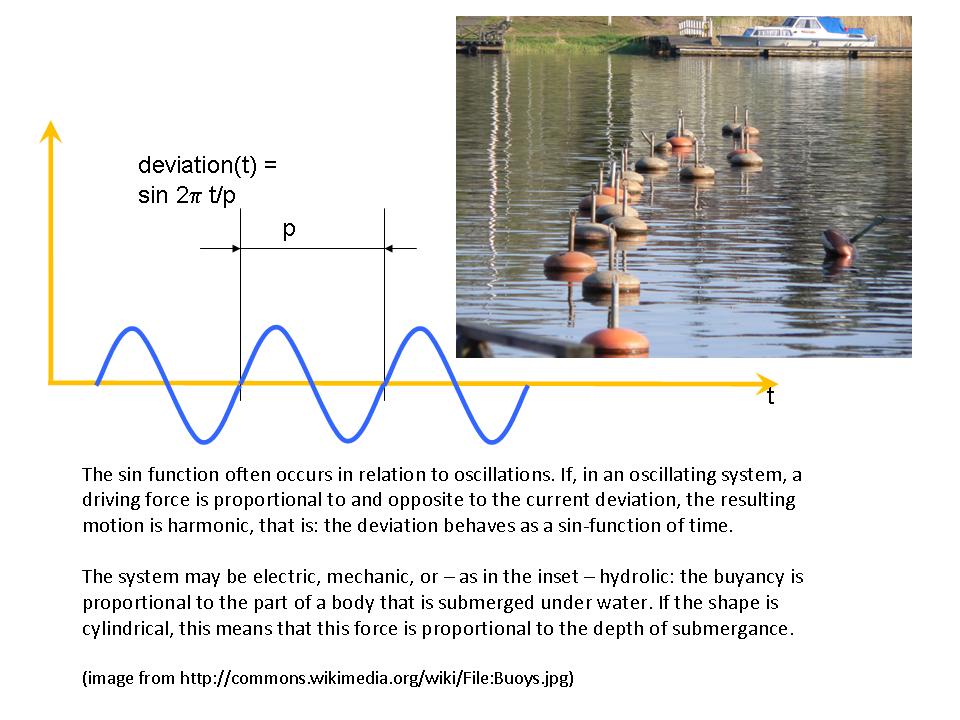
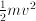 , for mass
, for mass 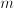 and speed
and speed 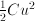 for spring constant
for spring constant  , where alternatingly one and the other dominates. In a circular motion (rotation), in hindsight, we also can identify periodic competition between two aspects: there, they are the vertical and horizontal deviation. If one is big, the other is small, and vice versa. This is the reason that oscillations are well described with complex numbers: the two competing aspects are the real and imaginary part of the complex number.
, where alternatingly one and the other dominates. In a circular motion (rotation), in hindsight, we also can identify periodic competition between two aspects: there, they are the vertical and horizontal deviation. If one is big, the other is small, and vice versa. This is the reason that oscillations are well described with complex numbers: the two competing aspects are the real and imaginary part of the complex number.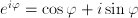 , which underlies all techniques for solving linear 2nd order differential equations – such as mass-spring systems and electric networks.
, which underlies all techniques for solving linear 2nd order differential equations – such as mass-spring systems and electric networks.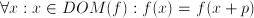 for constant
for constant .jpg)
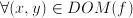 ,
, 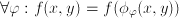 , where
, where 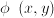 is a rotation over angle
is a rotation over angle 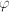 of the point
of the point 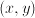 , then
, then 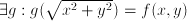 . Example: a rotational paraboloid,
. Example: a rotational paraboloid, 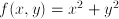 , is identical to
, is identical to 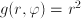 , where
, where 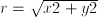 ; the latter function does not depend on
; the latter function does not depend on 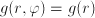 .
.
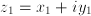 ,
, 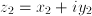 , their product is
, their product is 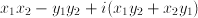 . The angle with the positive real axis of
. The angle with the positive real axis of 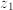 is
is 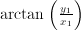 ; for
; for 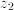 it is
it is 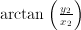 ; for
; for 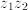 it is the sum of the two (follows from summation formula for
it is the sum of the two (follows from summation formula for 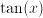 ). So rotating (in 2D) is the same as multiplying with a complex number with length 1 and angle with the positive real axis equal to the desired rotation angle.
). So rotating (in 2D) is the same as multiplying with a complex number with length 1 and angle with the positive real axis equal to the desired rotation angle.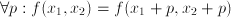 , then
, then 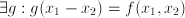 .
.
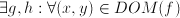 ,
, 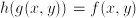 , then
, then 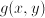 is the preferred quantity to work with rather than
is the preferred quantity to work with rather than .jpg)
 . There are two kinds of cholesterol, so two levels
. There are two kinds of cholesterol, so two levels 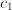 and
and 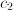 . It was very difficult to find a function
. It was very difficult to find a function 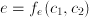 . It turns out, however, that there is a simple function
. It turns out, however, that there is a simple function 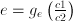 . Therefore,
. Therefore, 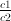 is a more meaningful quantity than
is a more meaningful quantity than 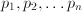 it is recommended to seek dimensionless quantities
it is recommended to seek dimensionless quantities 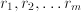
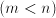 that each are a product of some of the
that each are a product of some of the 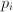 's (perhaps to some rational powers), and express
's (perhaps to some rational powers), and express 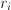 .
.
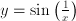 is differentiable but highly non-smooth; the function
is differentiable but highly non-smooth; the function 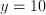 for
for  and
and 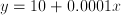 for
for 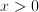 is not differentiable in
is not differentiable in 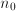 points, then the coarsest estimate of the perimeter is
points, then the coarsest estimate of the perimeter is 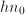 . Nest we halve
. Nest we halve 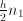 . This gives a sequence of estimates
. This gives a sequence of estimates 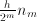 for
for 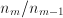 approaches 2. For very rough shapes, however, the ratio converges to a number larger than 2. The fractal dimension of the shape
approaches 2. For very rough shapes, however, the ratio converges to a number larger than 2. The fractal dimension of the shape 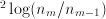 . For rough shapes, the fractal dimension is between 1 and 2; the larger the fractal dimension, the rougher the shape.
. For rough shapes, the fractal dimension is between 1 and 2; the larger the fractal dimension, the rougher the shape.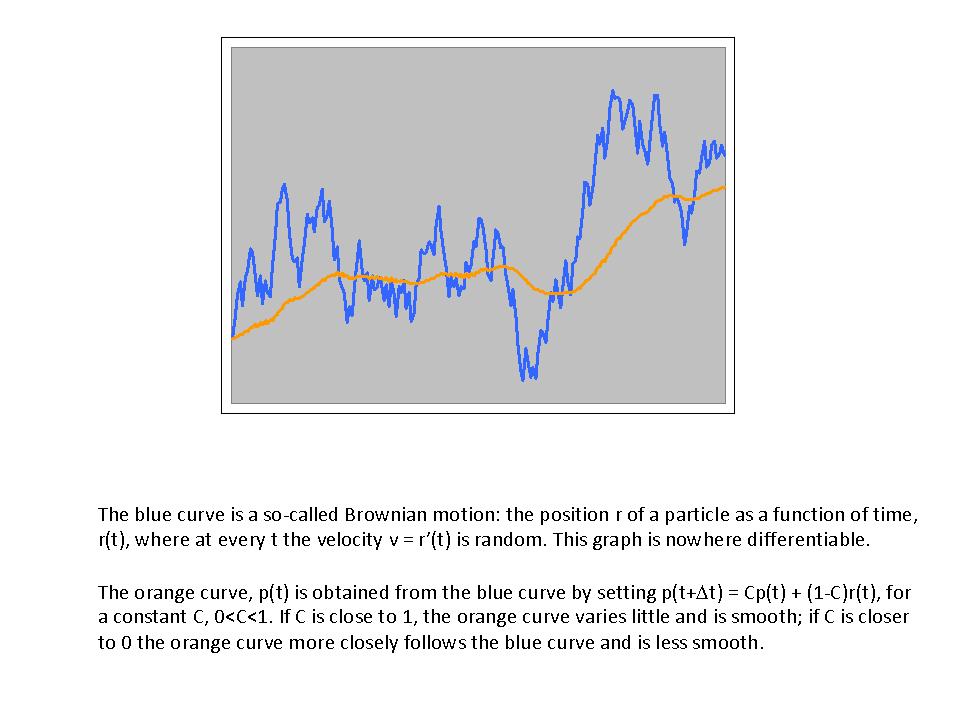
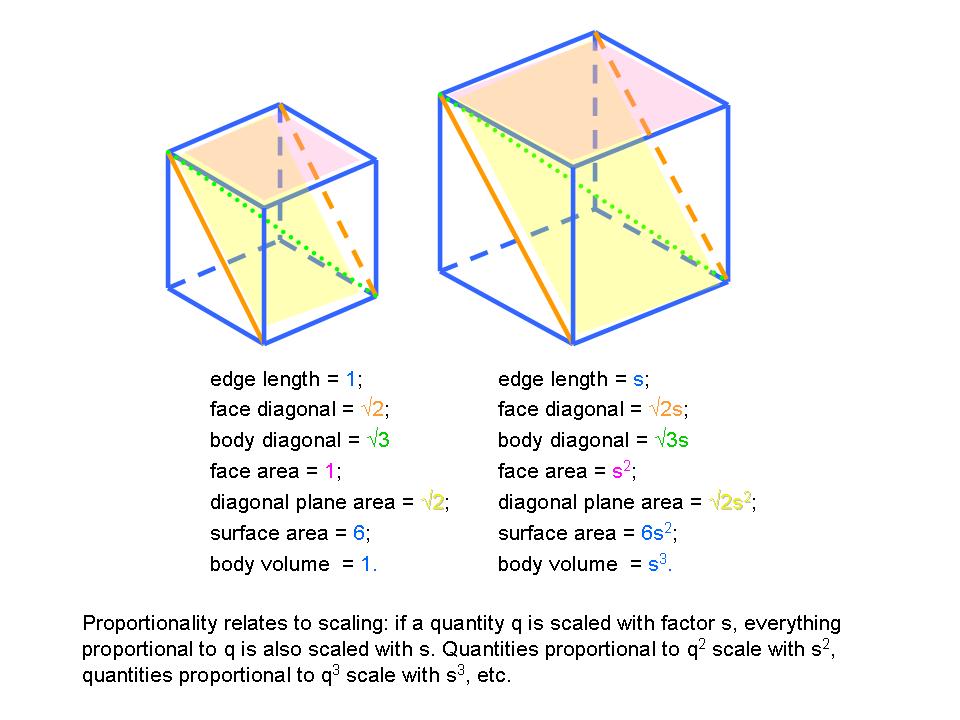
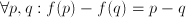 . Adding is commutative,
. Adding is commutative, 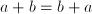 , and associative:
, and associative: 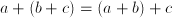 ; it distributes over multiplication:
; it distributes over multiplication: 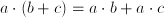
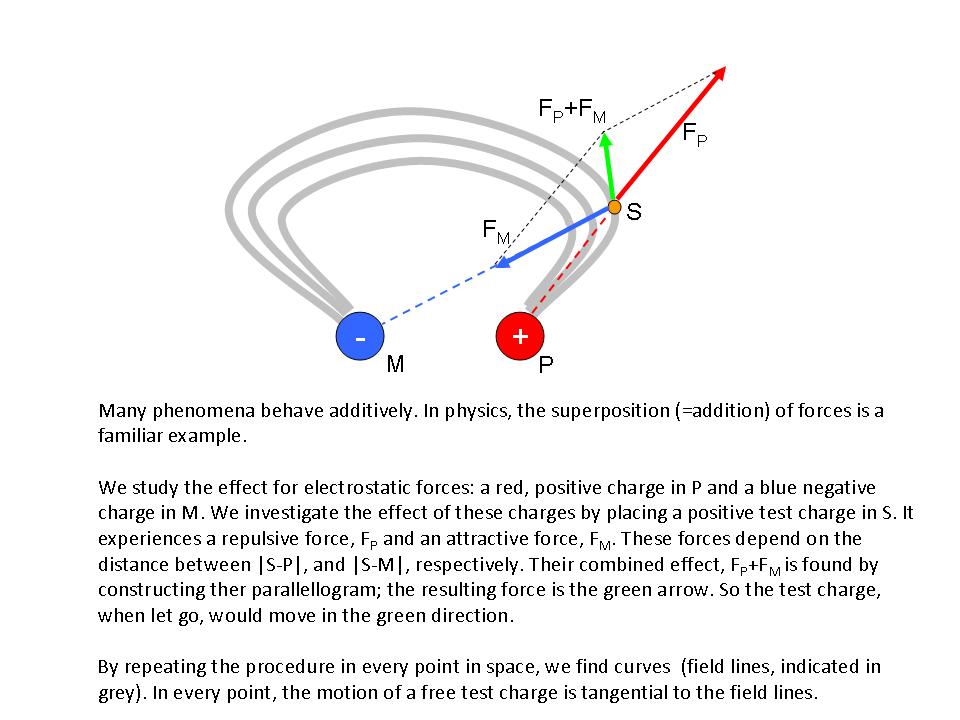
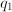 corresponds to phenomenon
corresponds to phenomenon 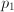 , and
, and 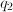 to
to 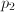 , the quantity corresponding to the two phenomena working simultaneously is
, the quantity corresponding to the two phenomena working simultaneously is 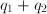 .
.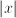 , gives a straight line; the slope of which is the power
, gives a straight line; the slope of which is the power 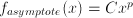 .
.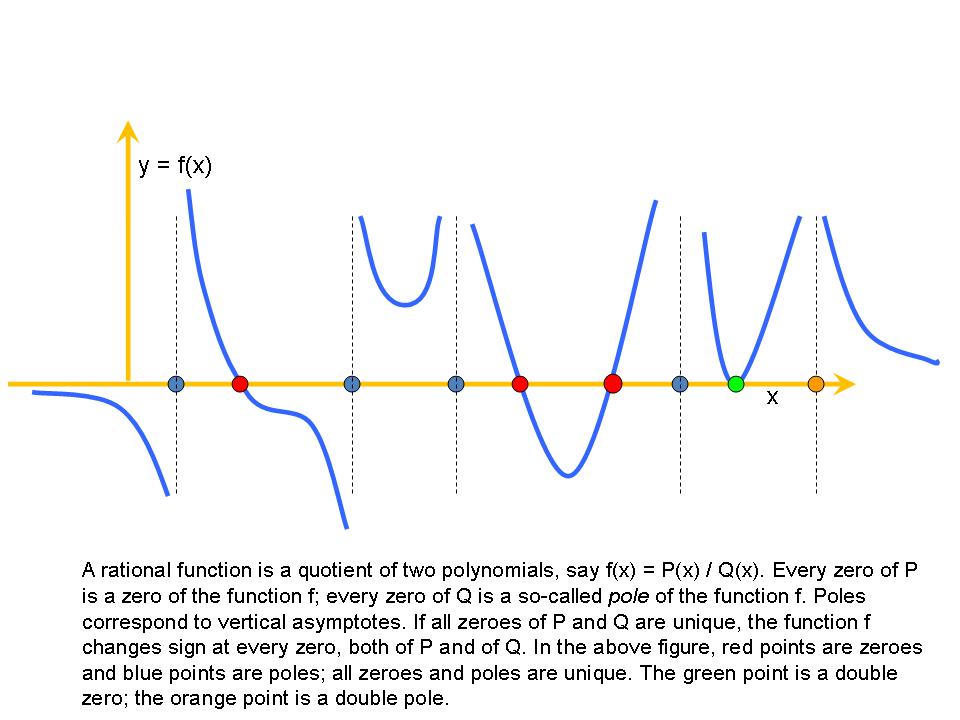
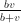 : a rational function of
: a rational function of 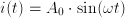 is given by the so-called transfer function
is given by the so-called transfer function 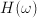 . This is a rational function of
. This is a rational function of 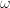 .
. ,
,  ,
,  and
and 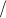 can be re-written to contain only one division, numerator and denominator being polynomials in
can be re-written to contain only one division, numerator and denominator being polynomials in 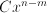 ,
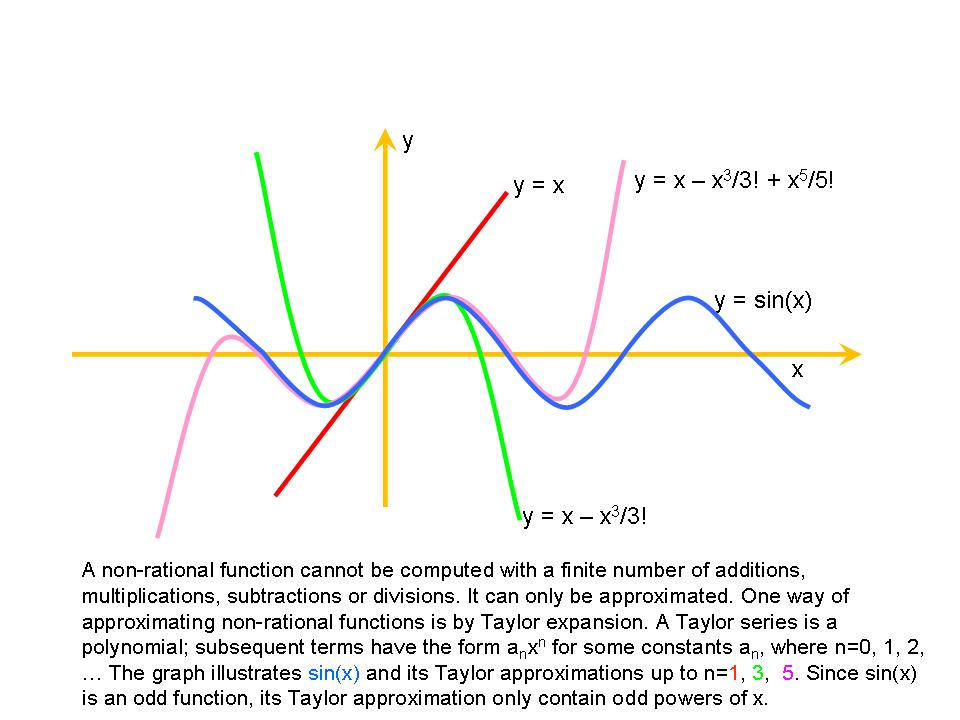
, 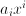 . Transcendental functions such as exp, log, sin etc. can all be defined as Taylor series with appropriate coefficients
. Transcendental functions such as exp, log, sin etc. can all be defined as Taylor series with appropriate coefficients 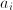 .
.
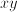 -plane.
-plane.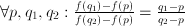 .
. 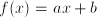 , so a can be found as
, so a can be found as 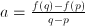 and
and 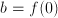 .
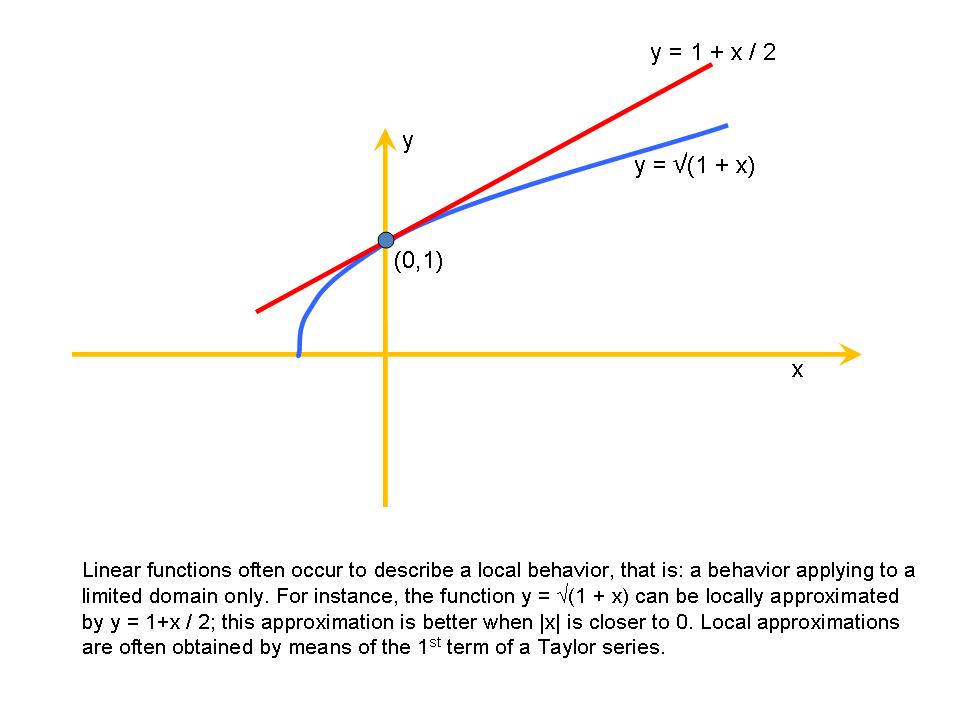
.
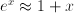 ,
, 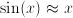 and
and 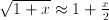 .
. , the function value
, the function value 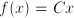 ; the dimension of
; the dimension of 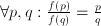 . Also:
. Also: 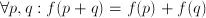 (although this equation, over
(although this equation, over 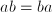 , and associative:
, and associative: 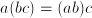 ; it does not distribute over addition:
; it does not distribute over addition: 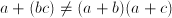
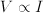 and
and 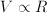 , hence
, hence  , and the constant of proportionality is 1
, and the constant of proportionality is 1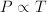 (pressure – temperature of an amount of gas with constant volume)
(pressure – temperature of an amount of gas with constant volume)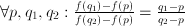 .
. 
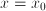 (sometimes called the equilibrium point, the starting position, the rest position, the start position, etc.),
(sometimes called the equilibrium point, the starting position, the rest position, the start position, etc.), 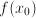 is the offset. The coefficient
is the offset. The coefficient 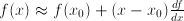
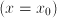 , the derivative
, the derivative  estimates the value of
estimates the value of 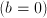 vs. inhomogenous
vs. inhomogenous 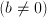 .
.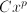 for either positive or negative
for either positive or negative 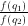 equals
equals 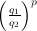 , so
, so 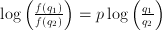 . In other words, plotting the log of the ratio of the function values agains the ratio of the arguments gives a straight line through the origin with slope
. In other words, plotting the log of the ratio of the function values agains the ratio of the arguments gives a straight line through the origin with slope 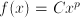 ,
,  . For arbitrary
. For arbitrary 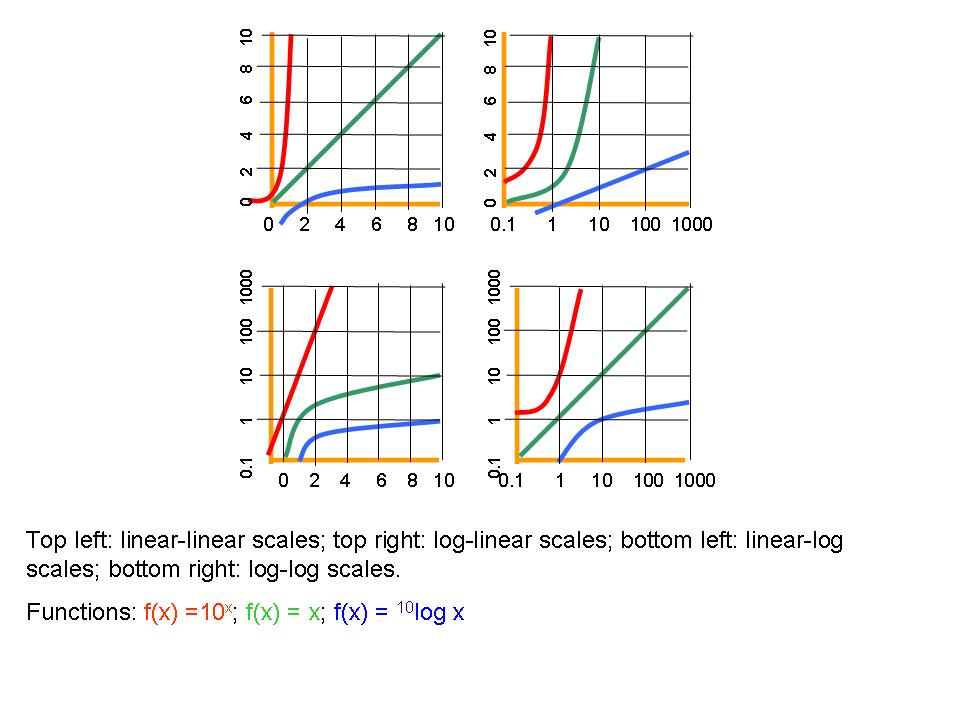
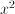 or
or 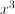 , respectively, with the size
, respectively, with the size 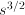 – which is a non-rational function of
– which is a non-rational function of 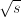 ; the amount of processing to sort
; the amount of processing to sort 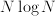 – which increases faster than proportional with
– which increases faster than proportional with 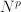 for any constant
for any constant  . For arbitrary
. For arbitrary 
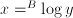 is the solution of
is the solution of 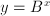 . Usually, base
. Usually, base 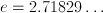 Let
Let 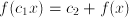 (
(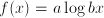 , we have that
, we have that 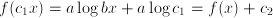 , so
, so 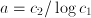 . The value of
. The value of 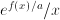 .
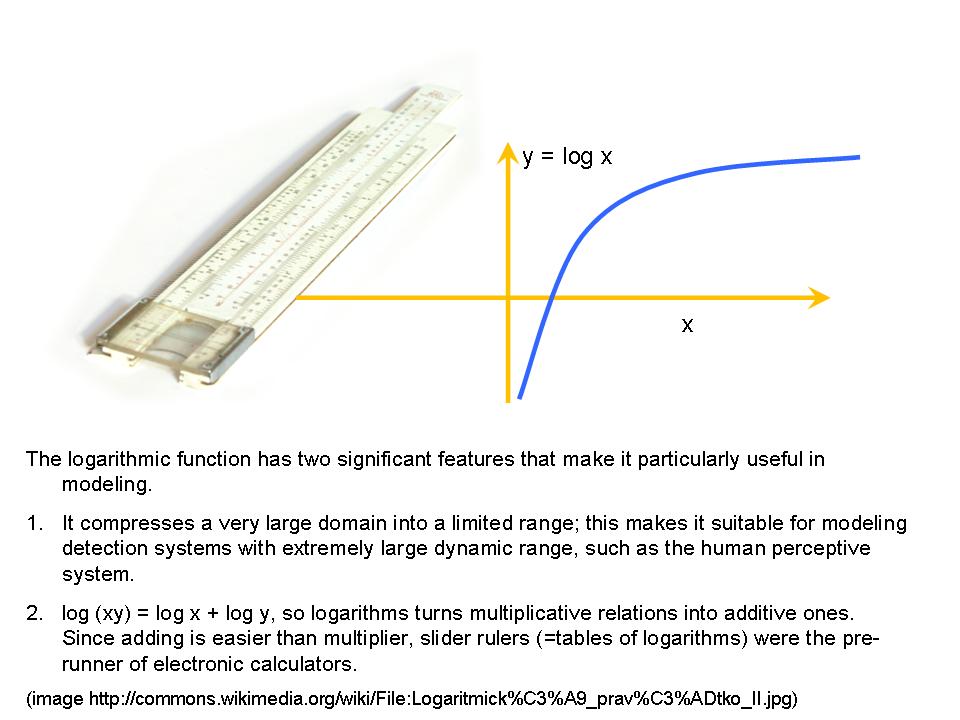
.
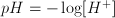 , where
, where 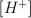 is the concentration of
is the concentration of 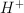 ions in a diluted solution. (Notice that one can argue whether or not
ions in a diluted solution. (Notice that one can argue whether or not 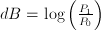 where
where 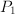 is some (audio) power to be measured and
is some (audio) power to be measured and 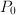 is a reference power.
is a reference power.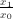 of input values
of input values 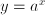 , can be written as
, can be written as 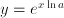 . Euler's constant,
. Euler's constant, 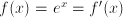 . For exponential behavior,
. For exponential behavior, 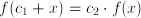 (
(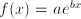 , we have that
, we have that 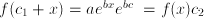 , so
, so 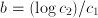 . The factor
. The factor 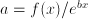 .
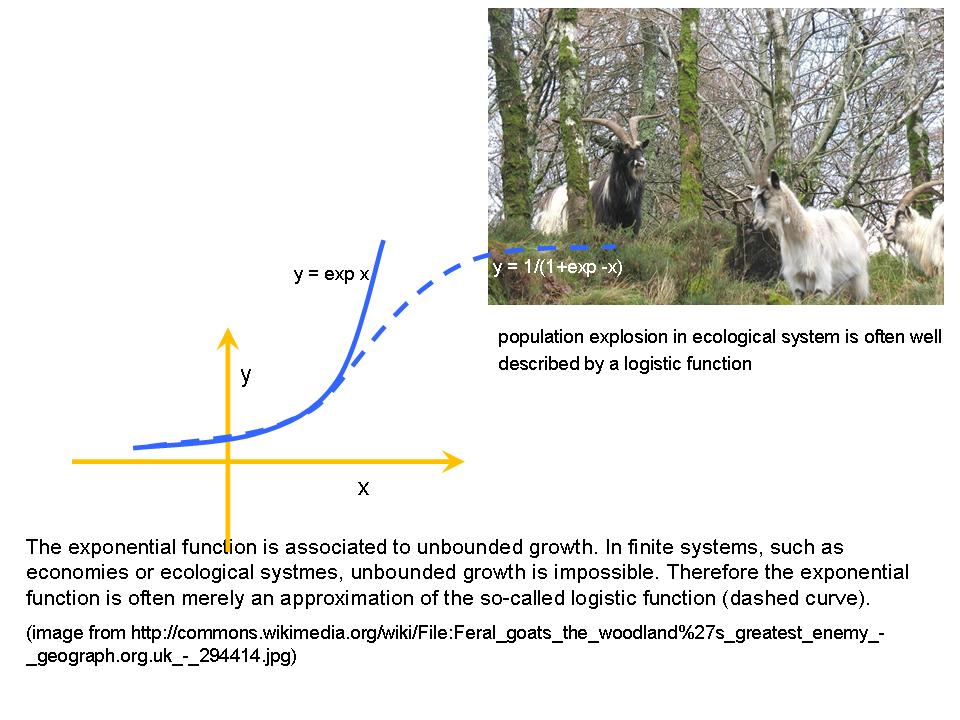
.
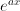 with
with  represents increase where a constant increment of the input causes multiplication by a factor in the output. If
represents increase where a constant increment of the input causes multiplication by a factor in the output. If 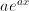 , the exponential function plays a crucial role in solving differential equations. Replacing the unknown function
, the exponential function plays a crucial role in solving differential equations. Replacing the unknown function 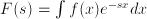 (this is the so-called Laplace transform) means that
(this is the so-called Laplace transform) means that 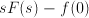 . Therefore the differential equation in
. Therefore the differential equation in 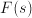 – which is much easier to solve. The resulting
– which is much easier to solve. The resulting .jpg)
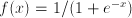 . Round
. Round 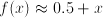 , but
, but 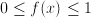 . Other applications of the logistic function include economics (price elasticity), chemistry, and physics.
. Other applications of the logistic function include economics (price elasticity), chemistry, and physics.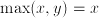 if
if 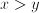 ;
; 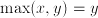 if
if 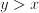 . The max function is commutative and associative:
. The max function is commutative and associative: 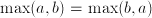 ;
; 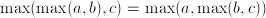 . Sometimes,
. Sometimes, 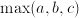 is used as abbreviation for
is used as abbreviation for 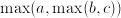 . The
. The  function can be defined as
function can be defined as 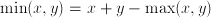 . The functions max and min are continuous but not differentiable in the situation where
. The functions max and min are continuous but not differentiable in the situation where 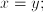 on left and right sides of this singularity, the derivatives are 1 and 0, respectively.
on left and right sides of this singularity, the derivatives are 1 and 0, respectively.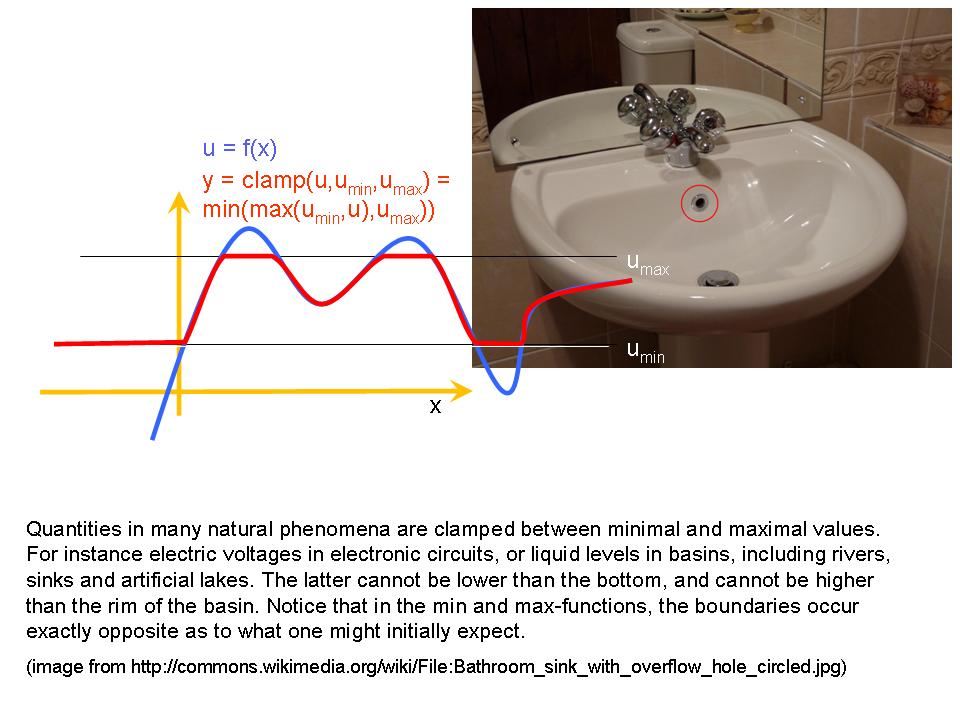
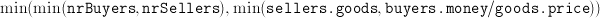 .
.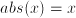 if
if 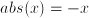 if
if 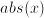 is continuous, but not differentiable. It is singular for
is continuous, but not differentiable. It is singular for 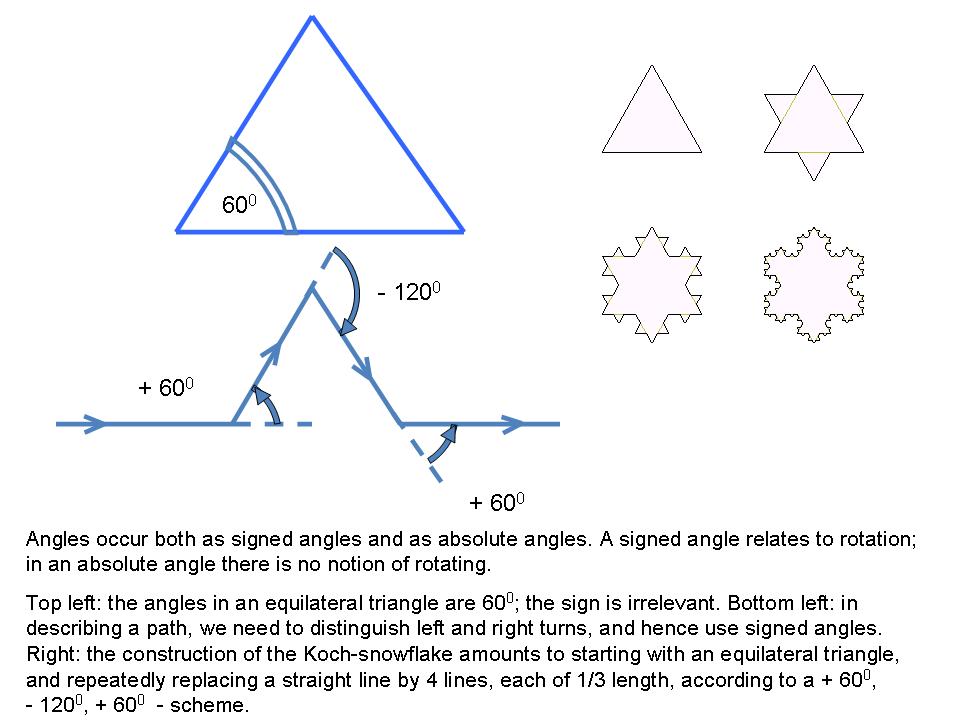
 and
and 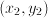 we may set
we may set 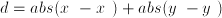 ; in another interpretation we may set
; in another interpretation we may set 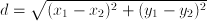 . In the first case, the points
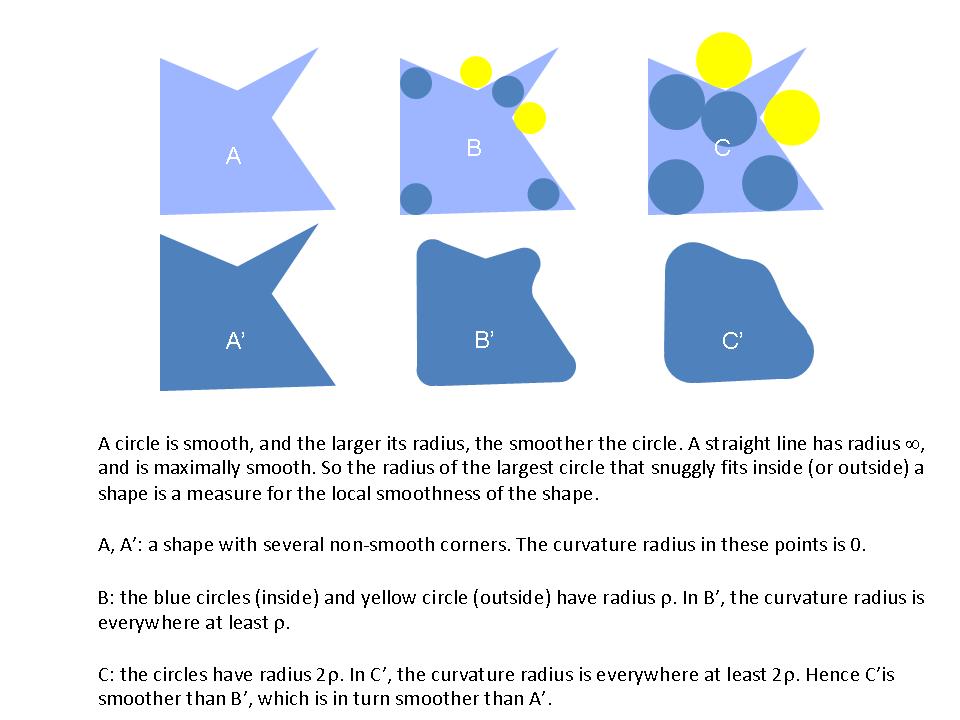
. In the first case, the points  . A continuous function that is non-smooth is either (in some points) not differentiable, or the radius of the largest touching circle (or ball) that stays on one side of the function graph (or surface) is zero.
. A continuous function that is non-smooth is either (in some points) not differentiable, or the radius of the largest touching circle (or ball) that stays on one side of the function graph (or surface) is zero..jpg)
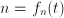 for a super market in depedence of the average transaction time
for a super market in depedence of the average transaction time 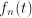 will be non-smooth.
will be non-smooth.